Find out Width of the belt:

An open flat belt drive is needed to transmit 20 kW. The diameter of one of the pulleys is 150 cm with speed equivalent to 300 rpm. The minimum angle of contact can be taken as 170^o. The permissible stress in the belt can be taken like 300 N/cm². The coefficient of friction among pulley and belt surface is 0.3. Find out

(a) Width of the belt neglecting influence of centrifugal tension for belt thickness equivalent to 8 mm.

(b) Width of belt letting the effect of centrifugal tension for the thickness equivalent to that in (a). The density of the belt material is equal to 1.0 gm/cm³.

Solution

In the question it is given that:          

Power transmitted (p) = 20 kW

Diameter of pulley (d) = 150 cm = 1.5 m

Speed of the belt (N) = 300 rpm

Angle of lap (θ) = 170^o = (170/180) π = 2.387 radian

Coefficient of friction (μ) = 0.3

Permissible stress (σ) = 300 N/cm²

(a) Thickness of the belt (t) = 8 mm = 0.8 cm

Assume higher tension is 'T₁' and lower tension is 'T₂'.

∴ T₁/ T₂  = e^μθ = e^{0.3 × 2.387}  = 2.53

The maximum tension 'T₁' is controlled through the permissible stress.

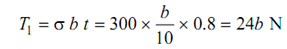
Where b is in mm

 Hence,

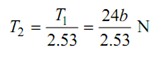
Velocity of belt V =

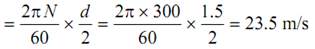
∴ Power transmitted

p =

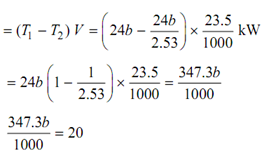
or,

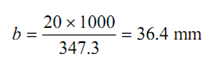
 (b) The density of the belt material (ρ) = 1 gm/cm³

Mass of the belt material/length m = ρ b t × 1 metre

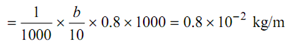
                                                               = 8b × 10^{- 3}  kg/m

 ∴ Centrifugal tension 'TC' = m V²

or,  T_C  = 8b × 10^{- 3} × (23.5)²  = 4.418b N

Maximum tension (T_max) = 24b N

∴  T₁ = T_max  - T_C  = 24b - 4.418b = 19.58b

Power transmitted P =

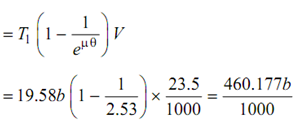
 Also   P = 20 kW

∴          460.177b /1000 = 20

or,        b = 45.4 mm

The effect of the centrifugal tension enhanced the width of the belt needed.