Path of Contact in Involutes Gears:

Assume two gears 1 and 2 with centres O₁ and O₂ mesh each other when transmitting motion as illustrated in Figure. The gear 1 is the driver and drives gear 2. The line EF is the common tangent to base circles of these both gears. The addendum circle of gear 2 meets common tangent EF at point C and this point shall be the begin of the contact of the two meshing teeth. The addendum circle of gear 1 meets EF at D and the contact shall terminate at this point. Thus, CD is the path of contact.

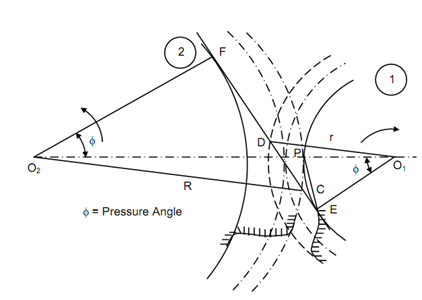
Let, r = the pitch circle radius of gear 1,

r_a = addendum circle radius of gear 1,

R = pitch circle of radius of gear 2, and

R_a = addendum circle radius of gear 2.

Path of contact = CD

CD = Path of approach + Path of recess

Or        CD = CP + PD CP = CF - PF

The triangle O₂ C F is a right angled triangle.

Thus,

 O₂ C ₂  = O₂ F ₂  + CF ₂

CF = (O₂ C² - O₂ F²  )^1/2

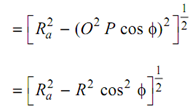
PF = O₂ P sin φ = R sin φ

Thus,   

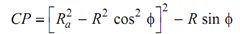
Likewise,

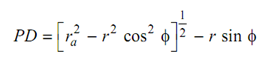
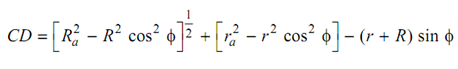. . . (9.3)