Cycloidal Profile Teeth:

In this kind of teeth, the faces are made up of epicycloids and flanks are built of hypocycloids.

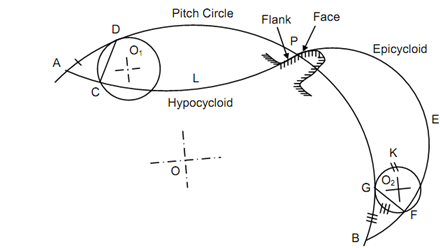
      Epicycloid, Hypocycloid and Generation of Cycloidal Profile Teeth

An epicycloid is the locus of a point on the circumference of a circle which rolls without slipping on the outside of the circumference of another circle in the similar plane. A hypocycloid is the locus of any point on the circumference of a circle which rolls without slipping inside the circumference of another circle in the similar plane. The formation of the cycloidal tooth profile has been illustrated in the Figure. A circle O₁ rolls inside another circle that is pitch circle of the gear. Since the circle O₁ rolls inside the pitch circle, it produced hypocycloid ALP. A small part of this curve near pitch circle is utilized for flank of the tooth. The normal to the hypocycloid at any point is the line joining the point along point of contact of the producing circle O₁ with pitch circle. In the similar way, if the circle O₂ rolls outside of the pitch circle, it produced epicycloids. The small part of this curve near pitch circle makes face of the tooth. Alike to the case of the hypocycloid, the line joining producing point having point of contact of the producing circle O₂ along pitch circle gives normal.

While motion is transmitted from one gear to another, the face of a tooth on one gear is in mesh along the flank of another tooth on the other gear. Thus, for proper meshing, it is essential that the diameter of the circle producing face of a tooth on one gear is similar as the diameter of the circle producing flank of the meshing tooth on another gear. This is illustrated in Figure

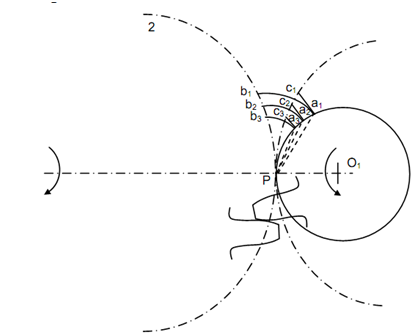
Let a generating circle O₁ which is rolling outside of the pitch circle of gear 2 and inside of the pitch circle of gear 1 .It shall generate epicycloids, a part of which is the face of tooth and gear 2. The flank of tooth on gear 1 is made up of hypocycloid that is produced by the similar circle by rolling inside pitch circle of gear 1. Consider a₁ be the creating point for epicycloid on pitch circle of gear 2 and hypocycloid inside pitch circle of gear 1. Both of these curves are created when O₁ rolls in clockwise direction. At beginning, a₁ coincide b₁ on 2 and c₁ on 1. At pitch point P the two pitch circles touch each other. while generating circle O₁ touches the pitch circle 2 at P, the creating point of epicycloid is at a₁ and line a₁ P is normal to the face of tooth on gear 2. Likewise, the creating point of hypocycloid is at a₁ and a₁ P is also normal to the flank of tooth on gear 1. Therefore, while face of tooth on gear 2 makes contact along flank on gear 1, a₁ P is the common normal at the point of contact. After that while point of contact is at a₂ then a2 P shall be common normal. While point of contact is at a₃, the common normal shall be a₃ P. The same will be the case while point of contact is on other side of P. The point of contact shall shift on the other producing circle. Now the face of the tooth of gear 1 shall touch the flank of gear 2.

      Transmission of Motion in Cycloidal Gears

The point of contact moves along the circumference of the two producing circles. Therefore, law of gearing is applied in case of cycloidal teeth.

Arc of approach = Arc a₁ a₂ a₃ P = Arc b₁ b₂ b₃ P = Arc c₁ c₂ c₃ P

The path of approach is equivalent to arc of approach.       

Likewise, it may be proved that the path of recess is equivalent to arc of recess. Thus, path of contact and arc of contact arc equivalent.

It may be observed from given figure that the pressure angle differs as point of contact moves. This is maximum at the starting of engagement and at the ending of engagement. It becomes zero at pitch point P. If the pitch circles don't touch each other law of gearing is not followed.