Maximum COP of the VARS

When the absorption system was to operate under ideal situations then its COP shall be the maximum. To visualize such an ideal situation all processes should be supposed to be reversible. The system operates constantly in a cycle with five interactions:

 Heat transfer Q_G to system at generator temperature T_G;
 Heat transfer Q_E to system at evaporator temperature T_E;
 Heat transfer Q_C from system at condenser temperature T_C;
 Heat transfer Q_A from system at absorber temperature T_A;
 Work transfer WP to the system at the pump.

Since the condenser and the absorber are cooled by the water from surroundings, for Ideal cases, TC = TA = TO the ambient temperature, and the total heat transfer to the surroundings = QO where

Q_O = Q_C + Q_A               ………… (i)

On applying the first law of thermodynamics to the system  

Q_O = Q_G + Q_E + W_P      ………… (ii)   

When the system was to be working reversibly the total entropy change of the system and surroundings would be zero. There can be no change in the entropy of the working substance as it endures a thermodynamic cycle. Therefore the total entropy change of the surroundings should be equivalent to zero.

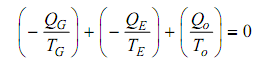
Replacing for Q_O in (iii) from (ii) and neglect W as small,   

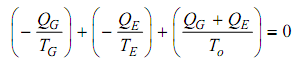
The equation (iv) can be simplified and rearranged as,

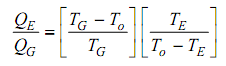
In equation (v) while the term on the left hand side is the COP of the system, the primary term on the right side is the Carnot effectiveness of a heat engine operating among the Generator and the ambient temperature and the second term is the COP of Carnot refrigeration system working among the evaporator and the ambient temperatures. Therefore, the maximum COP of an absorption system is equivalent to the product of the Carnot efficiency of a heat engine operating among T_G and T_O and the COP of a Carnot refrigerator operating among T_E and T_O.