Signaling game:

Here  we  analyze the  most  widely applied class of games  of incomplete information: signaling games. Stated abstractly,  a  signaling  game involves two players (one with private information, the other without) and two moves (first  a  signal  sent  by  the  informed player, then  a  response taken  by  the uninformed player). The key  idea is that communication can ocqur if one type of the  informed player is willing to send a signal that would be'too expensive for another type to send. We first define perfect Bayesian Nash equilibrium of signaling game and then give an example for it.  

Definition of Signaling Game

A signaling game is a dynamic game of incomplete information involving two players: a sender (S) and a receiver (R). The timing of the game is as follows:

1)  Nature draws  a  type  ti  for  the  sender  from  a  set  of  feasible types T = {t₁,  ...,  t_i) according to a probability distribution p(t₁), where p(t_i) > 0 for every i and  p(t₁)  +  ... + p(t_r)  = 1  .

2)  The  sender observes  ti  and  then chooses  a message mj  from  a  set of feasible messages M = {m₁,  ...,  m₂)  .

3)  The receiver observes mj  (but not  t,) and then chooses an action ak  from a set of feasible actions A = {a₁,  ....  a_k)  .

4)  Payoffs are given by U_s(t_i,  m_j, a_k) and U_R(t₁,  m_j,  a_k).

The figure below gives an extensive form  representation (without payoffs) of a simple case: T = (t₁,  t₂), M = (m₁,  m₂), A = (a₁,  a₂), and Prob(t₁) = p. Note that the play of the game does not  flow  from  an initial node at  the top of the tree to terminal nodes at the bottom, but rather from an initial move by nature in the middle of the tree to terminal nodes at the left and right edges.

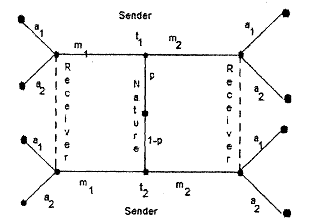
Before  we  go  to  give  the  formal  definition of  perfect  Bayesian  Nash equilibrium  of  signaling game,  we  must  give  four  requirements needed  to define perfect Bayesian Nash equilibrium of signaling game. Because  the sender  knows  the  full  history  of  the  game  when  choosing  a message, this choice occurs at a singleton information set. Thus, requirement 1  is  trivial when  applied to the  sender. The receiver,  in  contrast, chooses an action after observing the sender's message but without knowing the sender's type,  so  the  receiver's  choice  occurs  at a  nonsingleton information  set.