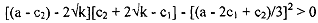Entry deterrence:

Here we want to emphasise a topic, that essentially an application of two stage game of perfect information viz. entry deterrence. Consider a situation where there are two  firms. Firm  1 is the  incumbent firm who  is already a monopoly in  the market  and  firm 2  in the potential new comer who wants  to enter into the market knowing the fact that firm  1 is already earning  supernormal profit due to her monopoly power. Assume both  firm produce homogeneous output. Also assume demand does not change over time. Now as firm  1 is a monopoly she can set  the market price  a she  like. But if the newcomer  firm  enter then she knows  that the market then become duopolistic. Assume that after the entry of the new  firm both will play  a Cournot Game. Then firm  1 no  longer being able to continue her monopoly. Therefore considering all this firm 1 can do  either  of  the  following  (1)  she allow firm  2  to enter  into the market and plays a Cournot Game or (2) she will decrease the price of her goods in such a way that  if the new comer firm enter and plays a Cournot Game then the new comer firm will earn zero profit and  therefore the new comer  firm will never enter.  The  second case constitutes  the case  for entry deterrence. There are many reasons why firms go for entry deterrence; firstly due to economics of scale in presence of large fixed cost, secondly due to absolute cost advantage may be due to superior technology.

Definition: Limit Quantity  (q_L)  is a quantity such that P(q+ q_L) < C(q)/q  for all q > 0,  i.e.  if the incumbent firm produce q~  then the potential entrance will make either zero profit or losses if she enter and produce any positive amount of quantity, where  P(Q)  is the inverse demand  hnction  and C(q)  is the cost fbnction of the new comer firm.  

Definition:  Limit Price  (p_L) is a  price such that P_L = P(q_L) where  q_i is the limit quantity. Now consider the following situation - Inverse demand function of the market  is given by  p = a -  q₁ -  q₂, where ql  is the quantity produced  by  the incumbent firm and q₂  is the quantity produced by  the new comer. Cost  function of  the incumbent firm  is Cl(ql)  = cl ql  and cost function of the new comer is C₂(q₂) =  c₂ q₂. Therefore, the profit function of the incumbent firm  is given by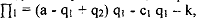

, where k is the fixed cost. Similarly, profit  function of the newcomer firm  is given by  n₂ = (a  - q₁  + q₂)  q₂  -  c₂  q₂  -  k. NOW suppose  incumbent  firm  allow  the new comer to enter into the market and therefore after entering the market both the firms will  plays Cournot game. Hence after entering the market both  firms will earn Cournot profit of duopoly, which is given by

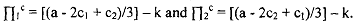
Now  suppose the  incumbent firm wants  to deter the entry  of  the  newcomer firm. Therefore, the incumbent firm should produce limit quantity. To find out the limit quantity  we  must  find  out a  particular quantity such  that  if  the incumbent firm produce  that  quantity  and  if  the new  comer  firm  will  enter then  for all positive quantity produced by  the new comer firm at that price will result non-positive profit.

We know that the reaction  function of the newcomer firm is given by - q₂  = [(a - c₂) - q₂]/2. By  putting this reaction function into the profit function of  the newcomer firm we have

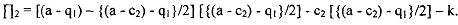
So, incumbent  firm  will produce such  a  q₁ such  that  n₂  = 0.  Therefore, solving this equation we have q, = (a - c₂)  - 2√k. NOW  if the incumbent firm will  produce this amount of quantity the best response of the newcomer  firm is  to not enter  in  the market, and  therefore producing zero output. So the total output  in  the market  is ql. And  therefore the  price in  the market  is p = c₂  + 2√k. Therefore profit of the  incumbent firm if she wants to deter entry is

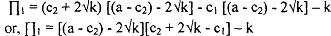
Now we know that the objective of the firm is to maximise her own profit and therefore the incumbent firm will deter entry of the new comer only if

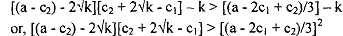
Therefore,  firm  1 (the  incumbent monopoly firm) will  deter the entry of the firm 2 (the potential new comer) if and only if