A Fuzzy Neural Petri Net System

In real-world situations here, the problem is to deal along with medical or engineering systems, some of the inputs as facts, evidences, and symptoms may be non-binary fuzzy variables in [O], [l]. A set of fuzzy rules of IF-THEN is generally employed to represent such systems. An illustration set of three rules is shown as:

R₁ : IF x₁ AND x₂ THEN y₁

R₂ : IF x₂ AND x₃ THEN y₂

R₃ : IF y₁ AND y₂ THEN g₁

The "IF" portion of a rule is known as the antecedent and the "THEN' part is termed as the consequent. The consequent and antecedent of rule may be single fuzzy variables or compound conditionals along with multiple propositions combined along with logical conjunction, negation or disjunction. The truth value of a rule shows the degree of belief in the fuzzy rule -larger the value, the more the rule is believed in. Conversely, the limitation the fuzzy rules have truth values greater than 0.5 has been normally adopted. A set of fuzzy rules is considered to be inconsistent if there is no interpretation that makes all the rules to concurrently have truth value greater than 0.5. Consistency is significant as no reliable information can be extracted from an information base that haves contradictions.

Generally, a fuzzy knowledge-base can be expressed like a set of R rules that employ a set of input variables (X), a set of hidden or intermediate variables (Y), and a set of output goals or variables (G). The inputs are usually independent, and such appear only in the antecedent part of the rule.

A goal or variable appears in at least one rule like a consequent and there is no rule in the rule set whether it appears as an antecedent. A set of rules might be interconnected in different possible manners.

A new class of Petri net named as Fuzzy Neural Petri Net or FNPN is explained in order to show a fuzzy knowledge-base and for reasoning in such a rule-based system. The Fuzzy Neural Petri Net is defined as a 7-tuple:

FNPN = {P, T , Z , C, V , α, β}

P = {P₁ , P₂ , ... , P_k } is a finite set of places,

T = {t₁ , t₂ , . . . , t_n} is a finite set of transitions,

Z is the finite set of arcs,

C = {X , Y , G} is a finite set of propositions,

Here,

X = {x₁ , x₂ , . . . , x_n } and Y = { y₁ , y₂ , ... , y_n } ,

G = {g₁ , g₂ , ... , g_n } ,

V = {v₁ , v₂ , ... , v_n} is a finite place of fuzzy truth values,

α= P → C is a mapping from places to propositions, and

β= T → V is relative function from transitions to truth values.

The places denoted via nodes represent the different transitions and the propositions represented via bars represent the rule along with truth values connected with them.

The initial marking of Fuzzy Neural Petri Net is the set of truth values linked with all source places or observations. A transition is enabled, whether for all input places there exists a token in place p_i and its truth value is greater than 0.5.

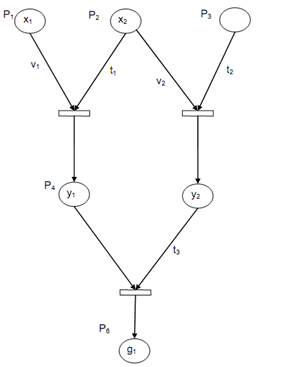
                                              Figure: A Fuzzy Pertinent Representing Three AND Rules

Above illustrates an example of a simple Fuzzy Neural Petri Net model showing the three rules. The places p_l to p₆ represent the propositions {x₁, x₂, x₃, y₁, y₂, g₁} and the transition set {t_l, t₂, t₃} shows the rules. Note that the transitions have an AND interpretation. The initial marking is the set of truth values [0, 1] linked with the observations x₁, x₂, x₃.

A fuzzy truth state component value x_i indicates the degree of belief in the truth of the subsequent proposition. The transitions t_l t₂ are enabled, if these truth values are greater than 0.5. A Fuzzy Neural Petri Net model for OR rules is shown in following figure.

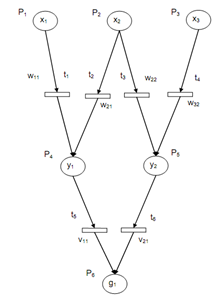
                                                      Figure: A Fuzzy Neural Pertinent Model for OR Rules

The consequent and the antecedent of a rule might be single fuzzy variables or compound conditions along with multiple propositions combined along with logical conjunction, negation and disjunction. Transformations of rules are possible such as there is a single proposition in the consequent part. For example, the rule IF x₁ AND x₂ THEN y₁ OR y₂, is equivalent to the rule IF x₁ AND x₂ AND y₂ THEN y₁. In the Fuzzy Neural Petri Net model, disjunctions and conjunctions of propositions are permitted in the antecedent part of a rule but merely disjunction of proposition are permitted in the consequent part. In order to accommodate negation, negative arcs along with label-1 may be employed. Previous figure shows rule transformation. Notice that the clausal form requires negation that is represented via negative arcs. Here a feed forward network based upon the neural network and fuzzy logic is employed.

The formalism of showing neural networks by Petri nets is represented. The trainable weights and thresholds are shown. The Fuzzy Neural Petri Net can be employed as a pattern classifier.

The Fuzzy Neural Petri Net can represent fuzzy rules and the truth value propagation. The Petri net model Fuzzy Neural Petri Net has practical importance as it employs discrete synaptic weights rather than varying synaptic weights. The memory needs is reduced also and the computations for Fuzzy Neural Petri Net are greatly simplified. Back-propagation-type training algorithms might be utilized for learning process.