Inclined Plane:

One of the simplest engineering devices for lifting loads to higher altitude is the inclined plane. The component of the weight of body along the inclined plane opposes if the body has to move up, and helps if it has to move down.

Consider a body resting on an inclined plane that is just on the point of moving down. The maximum angle of inclination at which this occurs is called the angle of repose.

As the body is just on the point of moving down, the direction of frictional force shall be acting up the inclined plane.

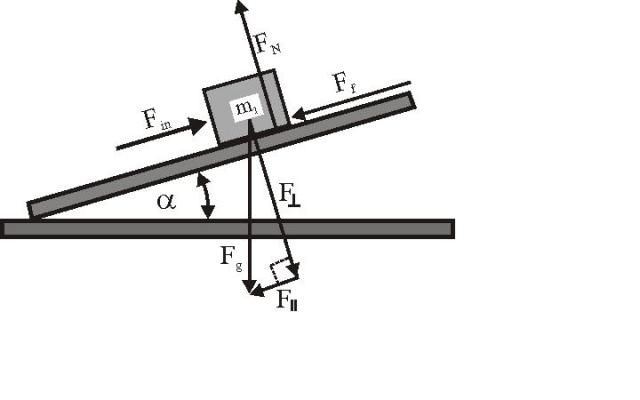
Resolving the forces along with and the normal to the inclined plane and by applying the conditions of static equilibrium, we obtain

 ∑ F_x  = 0

∴ F_A  = W sin α

∑ F_y  = 0

∴ N _A  = W cos α

But

 μ = F_A / N _A = W sin α / W cos α = tan α

It shows that the tangent of the angle of repose is equal to the coefficient of friction. Also, we know, μ = tan φ, where φ = angle of friction.

Hence, angle of repose is equivalent to the angle of friction.

If the angle of inclination α of the plane is less than the angle of repose φ, the body shall be at rest and an external force shall be needed to move it. If α > φ, then the body shall run down the plane and an external force shall be needed to prevent the body from running down.