Application of Method of Members:

Method of members as explained in the preceding section may be applied for solution of frames

Example

A billboard BC weighs 1000 N. It is subjected to a wind force of 300 N/m as illustrated in Figure. Neglecting weight of the supporting members, find out the hinge forces at A and F.

Solution

1. The hinge supports at A and F is replaced by horizontal and vertical components of reaction as shown in Figure. Therefore there are four unknowns and there are three possible equations and none of these unknowns may be determined by using them.

2. The free body diagrams of members ABE, BC, DEF have been drawn in Figure. At each hinge, the unknown hinge force is represented by two components. If the supposed direction is correct, the answer will be with positive sign while incorrect direction shall be suffixed with negative sign. The components of the hinge forces at C and D exerted by member CD are associated with the slope of CD in the original diagram since CD is loaded only at the hinges and therefore, transmits an axial force between C and D. The components of the hinge force and the two connecting members are in opposite sense. The action of the components of the hinge force at B on BC in part (a) are equal but opposite to action of these components upon AE in part (b). Likewise, at E components acting upon AE in part (b) are equal but opposite of these components working upon DF in part (c). Now the following table can be set up.

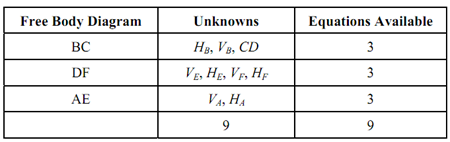
3.      For Member BC

3000 - H_B - H_CD = 0     . . . (a)

V_B - 1000 + V_CD = 0      . . . (b)

M_B = 10 H_CD - 3000 × 5 = 0     . . . (c)

∴          H_CD       = (3000 × 5) /10 = 1500 N, also, V_CD = 500 N

From Eq. (a),

H_B = 3000 - 1500 = 1500 N

 From Eq. (b),

V_B = 1000 - 500 = 500 N

For Member AE

- H _A + H _B + H _E = 0 ---- (d)

  V_A - V_B + V_E = 0--------- (e)

  M _A = - H _B × 4 - V_B × 6 + V_E × 12 - H _E × 8 = 0-------- (f)

For Member DF

- H _F - H _E + H _CD = 0------ (g)

+ V_F - V_E - V_CD = 0 --------- (h)

M _{F =} H _E × 4 - H _CD × 8 = 0         ---------- . (i)

4.        There are nine equations and nine unknowns. Therefore, the frame is statically determinate.

5.      From Eq. (i)

 H _E = H _CD (8/4) = 2 × 1500 = 3000 N

From Eq. (d)      - H _A + 1500 + 3000 = 0

Or     H _A = 4500 N

From Eq. (g) - H _F- H _E + H _CD = 0

or - H _F - 3000 + 1500 = 0

or - H _F= + 1500 N

or         H_F = 1500 N

From Eq. (e) V_A - V_B + V_{E =} 0

Or V_A + V_E = V_B = 500 N

From Eq. (f)

- 1500 × 4 - 500 × 6 + 12 V_E - 3000 × 8 = 0             --------- (j)

      V_E = + 33000 /12 = + 2750 N

Thus, from Eq. (j) V_A  = 500 - V_E  = 500 - 2750 = - 2250 N

Therefore, the reaction at A

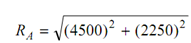
            = 5031.15 N

tan θ= 2250/4500  = 0.5

θ = 26.5^o                     Ans.

From Eq. (h) V_F   = + V_E + V_CD = + 2750 + 500 = + 3250 N

The reaction at F

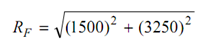
               = 3579.46 N

tan θ= 3250/1500  = 2.166

 θ = 65.22^o             Ans.