Fourier transform spectroscopy:

Fourier transform (FT) spectroscopy is a general concept used to study very weak signals after isolating it from environmental noise. It was first developed by astronomers in the early 1950s to study the infrared spectra of distant stars. In case of FT-NMR measurements, nuclei within a magnetic field are subjected to extremely brief pulses of intense radiofrequency radiation. This brief pulse of duration of few microseconds holds all the frequencies in the range where the nuclei can absorb. That causes all the nuclei in the sample to absorb the radiofrequency and get excited simultaneously. After a delay of a few seconds another pulse is applied. The delay is so chosen that during the interval between the two pulses all the excited nuclei relax back to the ground state and the population difference is achieved back. This relaxation is characterized by free induction decay (FID). This FID can be detected with a radio receiver coil which is perpendicular to the static magnetic field. In fact, a single coil is frequently used both to provide pulse to the sample and also to detect the FID signal. The FID signal is digitised and stored in a computer for data processing. The process of giving a pulse and collecting the FID takes a few seconds, therefore a large number of such FIDs which are in a way equivalent to a scan can be collected in a reasonable amount of time.

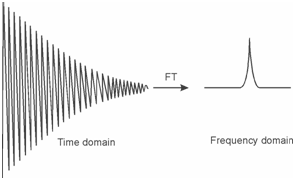
Figure: In Fourier transformation the time domain signal (FID) is transformed into a frequency domain signal

The time domain decay signals (FIDs) from numerous successive pulses are added to improve the signal to noise ratio. The resulting summed data are then converted to a frequency domain signal by Fourier transformation and finally, digital filtering may be applied to the data to further increase the signal to noise ratio. The resulting frequency domain spectrum is similar to the spectrum produced by a scanning continuous wave experiment. FT instruments have the advantage of high resolving power and wavelength reproducibility which make possible the analysis of complex spectra.