Decay And Half-Life:

The Radioactive substances steadily lose "potency" as time surpasses. Unstable nuclei disintegrate one by one. At times an unstable nucleus decomposes into a stable one in a single event. In other situations, an unstable nucleus changes into the other unstable nucleus, that later degenerate into a stable one. Assume that you have an tremendously large number of radioactive nuclei, and you measure the length of time needed for each one to degenerate and then average all the outcomes. The average decay time is termed as the mean life and is denoted by the lowercase Greek letter tau (Τ).

Some of the radioactive materials give off more than one form of discharge. For any given ionizing radiation form (alpha, beta particles, gamma rays, or other), there is an individual decay curve, or function of intensity versus time. The radioactive decay curve all the time has a characteristic shape: It begins out at a certain value and tapers down to zero. A few decay curves reduce quickly, and others reduce slowly though the characteristic shape is always similar and can be defined in terms of a time duration termed as the half-life, represented by t_1/2.

Assume that the intensity of radiation of a specific kind is measured at time t₀. Subsequent to a period of time t_1/2 has passed the intensity of which form of radiation reduces to half the level it was at t₀. After the half-life pass again (i.e., total elapsed time 2t_1/2), the intensity goes down to one-quarter of its real value. After so far another half-life passes (i.e., total elapsed time 3t_1/2), the intensity goes down to one-eighth its real value. In common, after n half-lives pass from the primary time t₀ (i.e., total elapsed time nt_1/2), the intensity goes down to 1/ (2ⁿ), or 0.5 n, times its real value. When the original intensity is x₀ units and the final intensity are x_f units, then

x_f = 0.5ⁿ x₀

The common form of a radioactive decay curve is shown in figure below. The half-life t_1/2 can differ extremely depending on the specific radioactive substance included. At times t_1/2 is a minute fraction of 1 second; in other situations it is millions of years. For each kind of radiation discharged by a material, there is an individual value of t1/2 and hence an individual decay curve.

The other way to define radioactive decay is in terms of a number termed as the decay constant, denoted by the lowercase Greek letter lambda (λ). The decay constant is equivalent to the natural logarithm of 2 (around 0.69315) divided by the half-life in seconds. This is stated as follows:

λ= 0.69315/t_1/2

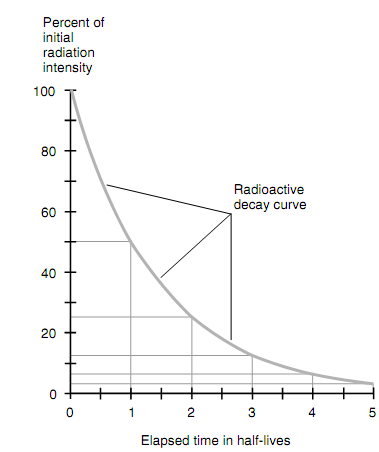
Figure: General form of a radioactive decay curve.

The symbol for the radioactive decay constant occurs to be similar as the symbol for EM wavelength. Do not mystify them; they are totally dissimilar and self-governing quantities. Also, whenever determining the decay constant, be certain that t_1/2 is stated in seconds. This will make sure that the decay constant is stated in the proper units (s^-1). If you begin with t_1/2 stated in units other than seconds, you will acquire a decay constant which is the incorrect number since it is stated improperly.

The decay constant is the reciprocal of the mean life in seconds. And hence, we can express these equations as:

λ = 1/ Τ and Τ = 1/λ

From such equations we can see that the mean life Τ is associated to the half-life t_1/2 as follows:

Τ= t_1/2/0.69315

  = 1.4427t_1/2

and

t_1/2 = 0.69315 Τ