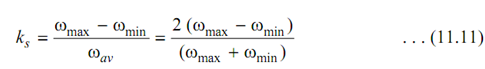Fluctuation of Energy and Speed:

As illustrated in Figures (a) to (d), the turning moment 'M' varies while the resisting moment considerably say 'M_R' that is because of the machine to be derived remains constant over a cycle for most cases. If we superimpose the resisting moment over the turning moment diagram, a situation illustrate in Figure will arise. If MR is equivalent to the average turning moment (Mav), energy available will be equivalent to the energy needed over a cycle. It may be observed that for some values of θ turning moment is more than M_R and for some values of θ turning moment is less than M_R.

The energy output can be defined mathematically as follows :

E = ∫ M d θ

The average turning moment for the cycle is following

 M _av = E/ Angle for cycle

The angle for the cycle is given as 2π for the two stroke engines and 4π for four strokes engines.

For a constant operation of the system

M_R = M_av

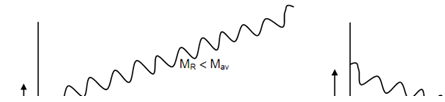
In the stable system, the mean speed remains stable but variation of speed shall be there in the cycle. The speed remains similar at the starting and at the ending of the cycle.

If M_R < M_av, the speed increases from cycle to cycle. The speed graph is illustrated in

Figure (a).

If M_R > M_av, the speed reduced from the cycle to the cycle. The speed graph is illustrated in Figure (b).

 (a)                                                         (b)

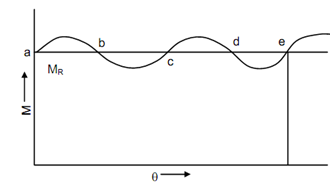
From previous Figure, we observe that M_R = Mav at points a, b, c, d and e. As M > M_R through a to b, speed of the crank shaft shall increase throughout this period. From b to c M < M_R and speed shall decrease. Similar circumstances will take place for c to d and d to e. At e the cycle is finished and the speed at e is similar as that of a. The energy at all of these points can be determined.

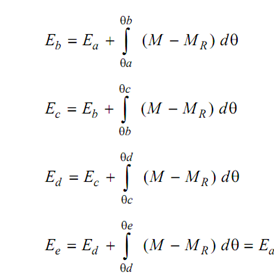
Out of all these energies so resolute, we can discover minimum and maximum energies, the difference in these energy levels will give maximum fluctuation of energy (Δ E)_max

                                                (Δ E )_max  = E_max  - E_min

The coefficient of fluctuation of energy means to the ratio of maximum fluctuation of energy to the energy of cycle

∴          k_e = (Δ E)_max/ E                                 . . . (11.10)

 The maximum energy level point will have maximum speed and minimum energy level point will have minimum speed. Following are coefficient of fluctuation of speed