Estimates mass moment of inertia:

The turning moment figure for a multi cylinder IC engine is drawn to the given scales

1 cm = 15^o crank angle

1 cm = 3 k Nm

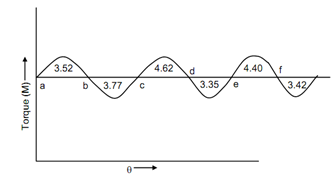
Throughout one revolution of the crank the areas having reference to the mean torque line are 3.52, (-) 3.77, 3.62, (-) 4.35, 4.40 and (-) 3.42 cm2. Estimates mass moment of inertia to keep the fluctuation of mean speed in ± 2.5% with reference to mean speed. Engine speed is equal to 200 rpm.

Solution

The turning moment diagram is illustrated in Figure. The scales are given as

1 cm = 15^o crank angle

1 cm = 3 k Nm

 Hence,

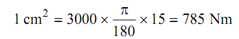
The total speed fluctuation = 2 × 2.5%

∴          Coefficient of speed fluctuation 'k_s' = 0.05

Engine speed = 200 rpm

∴       

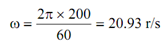
Assume Energy level at a is 'E' cm²   

Energy level at b is E_b = E + 3.52

Energy level at c is E_c = E_b - 3.77 = E + 3.52 - 3.77 = E - 0.25

Energy level at d is E_d = E_c + 3.62 = E - 0.25 + 3.62 = E + 3.37

Energy level at e is E_e = E_d - 4.35 = E + 3.37 - 4.35 = E - 0.98

Energy level at f is E_f = E_e + 4.40 = E - 0.98 + 4.40 = E + 3.42

Energy level at g is E_g = E_f - 3.42 = E + 3.42 - 3.42 = E

Energy level at the ending of cycle and at the starting of the cycle should be similar. By comparing the values of energies at several points, we get following

Maximum energy is at 'b', that is E_max = E + 3.52

Minimum energy is at 'e', that is E_min = E - 0.98

 Since,

∴ Δ E = I k_s  ω²

3532.5 = I × 0.05 × (20.93)2