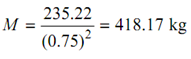Estimate the mass of the flywheel:

A single cylinder four-stroke petrol engine produced 18.4 kW power at a mean speed of 300 rpm. The work done throughout and exhaust and suction strokes may be neglected. The work done by the gases throughout explosion strokes is three times the work done on the gases throughout the compression strokes and they may be represented by the triangles. Estimate the mass of the flywheel to prevent a fluctuation of speed greater than 2 per cent from the mean speed. The flywheel diameter might be taken as 1.5 m.

Solution

Power developed 'P' = 18.4 kW

Mean speed 'N' = 300 rpm

Fluctuation of speed = ± 2%

Diameter of flywheel = 1.5 m

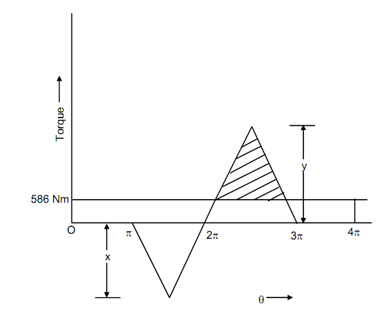
The turning moment diagram is illustrated in Figure

Assume height of the triangle in compression stroke by 'x' and that is in explosion stroke be 'y'. As work done in explosion stroke is three times to that in compression stroke.

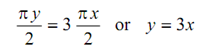
The net work done per second = 18.4 × 1000 Nm

Numbers of cycles per second = 300 /(60 × 2) = 2.5

Thus, work done per cycle = 18400 /2.5 = 7360 Nm

From turning moment diagram, work done per cycle =

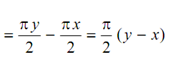
Or

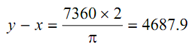
By putting for y in the above expression.

3x - x = 4687.9   or x = 4687.9 /2

or,        x = 2343.95 kN

∴          y = 3x = 7031.85 Nm

Average net torque = 7360/ 4π = 586 Nm

The fluctuation of energy shall be provided by the shaded area illustrated in Figure. From the theory of same triangles

Thus, fluctuation of energy Δ E = (2.878 × 6445.85) /2= 9276.63 Nm

Δ E = I k_s  ω²

k_s  = 2 × 2% = 4% = 0.04

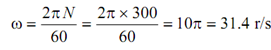
∴          9276.63 = I × 0.04 × (31.4)²

or,

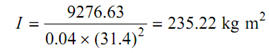
Supposing that the entire mass is concentrated at the rim

                                    I = M R²

here R is radius of the rim.

R = 1.5/2 = 0.75 m

∴          235.22 = M (0.75)²