Estimate Moment of inertia of the flywheel:

The resisting torque on the crank of a riveting machine is given as 200 Nm for first 90^o, from 90^o to 135^o is given as 1600 Nm then it drops linearly to 200 Nm up to 180^o and remains the similar upto 360^o. The period of cycle is 2 sec. The motor throughout the machine, yet, has a speed of 1450 rpm and it delivers constant torque. The crank shaft of the machine is geared to the motor shaft. The speed fluctuation is restricted to ± 2% of mean speed. Estimate:

(1) Power of the motor, and

 (2) Moment of inertia of the flywheel mounted on the motor shaft.

Solution

In this, torque supplied is constant and demand torque is fluctuating. The demand torque is illustrated in Figure

 (a) The energy needed per cycle

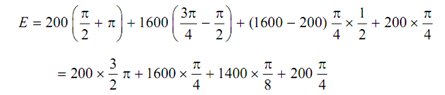
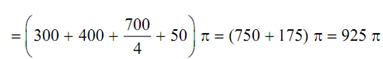
               = 2904.5 Nm

The period of the cycle is 2 seconds

∴          Energy required per second = 2904.5/2 = 1452.25

∴          Power of motor required, p = 1.452 kW.

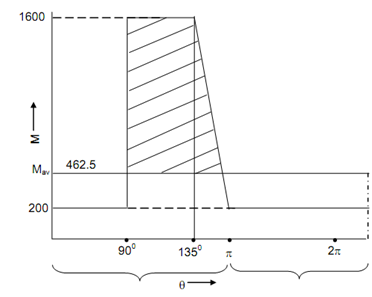
(b)        The average torque M _av = E /2π = 2904.5 / 2π

 or,       M_av = 462.5 Nm

The shaded portion is fluctuation of energy. Thus,

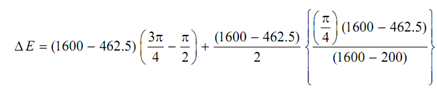
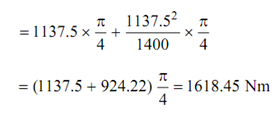
Δ E = I k_s  ω²

ω= 2π N/60

  = (2π × 1450 )/60 = 151.76 r/s

Coefficient of speed fluctuation k_s

= (2 × 2) /100 = 0.04

∴          1618.45 = I × 0.04 × (151.76)²

or,

 I =       1618.45 /(0.04 × 23032.1) = 1.76 kg m²