Dynamically Equivalent System:

The slider-crank mechanism is one of the most commonly utilized mechanisms. It is utilized into prime movers, punching press, reciprocating compressors etc. The reciprocating mass involves mass of the piston and partition of the mass of the connecting rod. One ending of the connecting rod reciprocates having cranked. We need to replace this link by a mass less link that is dynamically equivalent having two point masses m₁, at the piston ending and m₂ at the crank ending.

In a general case, we may think of a rigid link of any shape as illustrated in Figure. Let this be subjected to a system of forces whose resultant is say 'F' producing a couple F_e regarding centre of gravity G. This force generates linear acceleration 'a' ( = F /m)   and

angular acceleration 'α' ( = F _e /I) , where I is mass moment of inertia around a perpendicular axis through G.

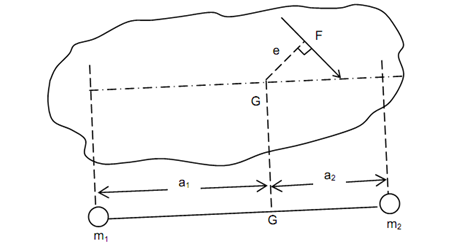
For the massless link with point masses m₁ and m₂ to be dynamically equivalent, this must generate similar accelerations 'a' and 'α' because of the action of similar force 'F'.

Assume a₁ and a₂ be the distances of the point masses m₁ and m₂ respectively from centre of gravity G.

For a dynamically equivalent system with accelerations 'a' and 'α'

(a) Total mass must be similar, that means

                                    m₁ + m₂ = m                                           . . . (11.1)

 (b) Position of centre of gravity must remain similar, that means

                                   m₁ a₁ = m₂ a₂                                                                      . . . (11.2)

 (c) Mass moment of inertia should be similar, that is                                           

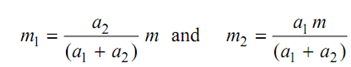                    . . . (11.3)

These three equations (11.1) to (11.3) must be satisfied for total dynamical equivalence. There are four unknowns (m₁, m₂, a₁ and a₂) and the three equations. Thus, one of these four variables may be arbitrarily supposed and other three can be estimated to provide a unique solution.

For slider-crank mechanism, it shall be convenient to contain mass m₁ along the piston and mass m₂ at the crank ending and therefore a₁ and a₂ are decided beforehand. But in that case all of the three equations cannot be satisfied.

From equation (11.1) to (11.3),

and mass moment of inertia = m a₁ a₂.

If masses m₁ and m₂ are situated at above mentioned positions the equation (11.3) will not be satisfied. The change in moment of inertia shall be

                                     = I - m a₁ a₂

                                     = m k ² - m a₁ a₂ = m (k ²- a₁ a₂)

The correction couple needs to be determined and it will be m (k ² - a₁ a₂) α. This couple may be thought of applied by the two forces F_C as illustrated in given figure.

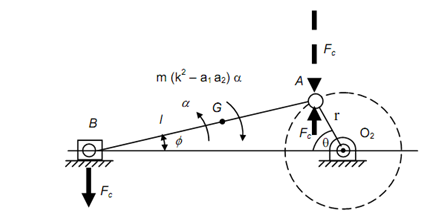
Hence ,

 F_C  l cos φ= m (k ²  - a₁  a₂ ) α

or,

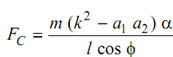                          . . . (11.4)

The correction in the turning moment shall be equivalent to the moment of force F_C illustrated by the dashed line regarding the crank centre.

 Correction couple =- F_C r cos θ

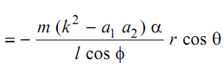
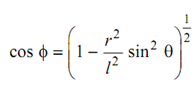
Applying Different ion twice w.r.t. 't' and letting 'ω' constant

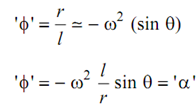
Correction couple

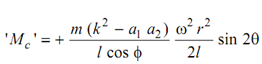                        . . . (11.5)