Bernoulli's Equation:

To derive Bernoulli's equation, let us consider a tube AB in which a liquid is flowing as streamline flow (Figure). Let the density of the liquid is ρ and the heights of points A and B above ground level be h₁ and h₂ respectively. Let a₁ and a₂ be the areas of cross-sections of the tube at points A and B and p₁ , p₂   be the pressures and v₁, v₂ be the velocities of flow at these points respectively.

Since the flow of liquid is streamline and in view of the equation of continuity, the net result of liquid flow in a time interval δt is transfer of mass, say m, from point A to point B. The question is: How much work is completed on the liquid of mass m and what is the change in its kinetic energy when it is transferred from point A to point B?

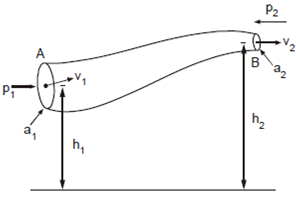
Figure: Streamline Flow of Liquid through a Tube of Different Cross-sectional Areas at difficult Heights from the Ground Level

To find an answer to these questions, we required to

(a) Calculate the change in the kinetic energy of mass m of the liquid in moving from point A to B, and

(b) Compute the work done on the system (mass m of the liquid) by

(i) Pressure difference among points A and B, and

(ii) The gravity.