Example of Machine -Loading Problem of Random FMS

Let's consider an instance of machine -loading problem of random FMS in which 8 part kinds are to be processed on four machines, each with five tool slots & different processing time for each of operation. Each part kind consists of necessary and optional operations, which might be performed on any of the machine without modifying the sequence of the operations. The adaptability of each of machines and its potential to perform various different operations facilitate various operation assignments to be duplicated to produce alternative part routes. Therefore, there can be fairly large number of combinations in which operations of the part type might be assigned on the different machines while satisfying all of the technological and capacity constraints. Additional consideration of flexibilities such like: part movement flexibilities, tooling flexibilities, etc. along with the constraints of the system configuration & operational feasibility make the problem more difficult.

To arrive at optimal or nearly optimal solution for the machine loading problem, combinations of machines & operations allocated are evaluated by using two common performance measures: system unbalance, and throughput. This is necessary to explore each of combinatorial allocation with respect to a given objective function (minimization of system unbalance & maximizing throughput), by satisfying constraints simultaneously. This is found that number of possible allocations, to be explored, enhance exponentially as size of the problem enhance.

                                                                   Table  : Description of Problem No.1

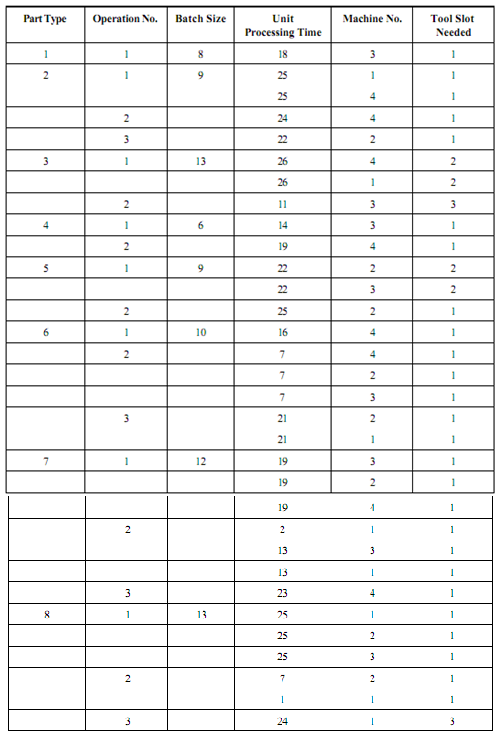
Various researchers have solved machine loading difficulty by generating the pre- determined part sequencing based heuristics, however these techniques don't guarantee optimal/near optimal solutions. Thus, the application of local intelligent search techniques, such like tabu search (TS), simulated annealing (SA), genetic algorithm (GA), and CBGA (Constraint Based Genetic Algorithm) have been widely used by researchers since the year 1992, to solve such a computationally complex optimization problem.

These difficulty have been addressed considering following objective functions:

1. Minimization of system unbalance alone;

2. Maximization of throughput alone; and

3. Minimization of system unbalance and maximization of throughput considered together.

Let us solve out the above problem by using an evolutionary heuristic known as Reallocation paradigm. An approach that ensures simultaneous allocations of an index of essential in addition to optional operations on the machines depend on the value "operations allocation priority index" has been pursued. The concept of "operation allocation priority index" (PI) has been evolved to include the effects of available and essential time and tool slots on the machines before & after the operation decision of a part type.