General Case of Fixed Beams:

Using the result of Example, we could solve most of the problems of fixed beams subjected to any type of loading as shown below.

Find the fixed end moments and draw the BM and SF diagrams for the fixed beam shown in Figure 14. EI is constant for the beam.

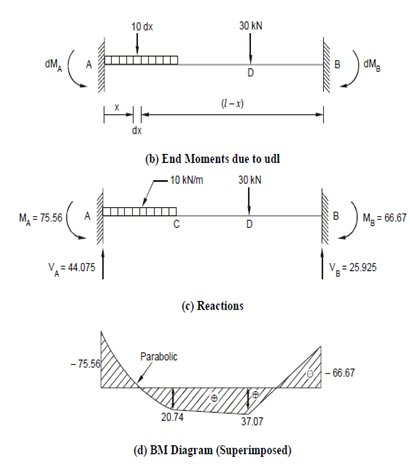
Solution

From Example 2.5, for the concentrated load

M_A =- (30x8x4²)12² =- 26.67 kNm

M_B = - (30x8²x4)12² = - 53.33 kNm

For the uniformly distributed load, we consider a small width dx at a distance x from A (Figure 14(b)), the load on this small strip is 10 dx and may be assumed concentrated at this point, the elemental fixed end bending moment dM_A due to this load will be

dM_A  = -(10 dx) x (12 - x) ²/12²

Integrating both sides within limit x = 0 to x = 4.

We have

∫ dM_A =- 1/12² ∫⁴₀ (10 dx)x(12-x)²

M_A =- 1/12² ∫₀ 10x(144-24x+x²)dx

=- 1/144[1440 x²/2 -240 x³/3 +10 x⁴/4]⁴₀

=- 1/144 (1440x16/2-240x64/3+2560/4)

=-48.89 kNm

Similarly, dM_B  =-(10 dx) x² (12-x)/12²

Integrating M_B =-∫ (10 dx) x² (12-x)/12² =-10/144 ∫⁴₀ (12x² - x³)dx

=- 10/144[12.x³ /3 - x⁴ /4 ]⁴ =- 10/144 [4x4³ -4⁴/4]

= - 13.33 kNm

Adding the moments due to both u. d. l. and concentrated load we get M_A = - (26.67 + 48.49) = - 75.76 kNm and this is anticlockwise at left hand end (because a hogging bending moment).

M _B = - (53.33 + 13.33) = - 66.66 kNm and this is clockwise at right hand end again (because a hogging bending moment).

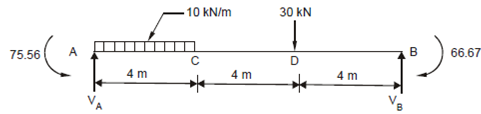
The free body diagram is shown in Figure.

Vertical reactions VA and VB are now obtained by the conditions of static equilibrium.

∑ M = 0.

Taking moments of all the forces and couples about B, we have

 V_A × 12 - 75.56 + 66.66 - 40 × 10 - 30 × 4 = 0 ; giving V_A = 44.075 kN ↑ .

Similarly, ? ∑V ≡ 0 ⇒ V_A  + V_B  = 10 × 4 + 30 ; giving V_B = 25.925 kN  ↑ .

The BM diagrams are shown in Figures (d) and (e) and the SF diagram in Figure (f) which may be verified.