Example of analysis of a fixed beam:

Now let us take the example of analysis of a fixed beam AB which carries a single concentrated load P at distance a and b from the ends A and B respectively (span l = a + b, and EI of the beam is constant).

Solution

The free BM diagram is shown in Figure 13(b). It is a triangle with maximum ordinate Pab  / l at the point C (below the load).

Supposing the fixed end moments which are negative as - MA and - MB the fixed BM diagram is a trapezium as shown in Figure 13(c).

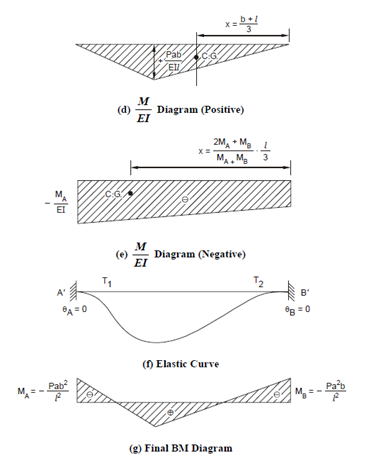
As EI is constant, the M/EI diagrams are similar and shown in Figures 13(d) and (e).

Now to search the unknown end moments A and B we have the following two conditions of compatibility:

(a)        The modify of slope from A to B is zero since both the slopes are zero.

(b)       A intercept of the tangents at A and B on a vertical line through B is zero since both the tangents are horizontal and at the same level.

Now, applying the moment area theorem to this condition:

(a)        The first condition implies that the net area of the M/EI   diagram from A to B is zero, i.e. area of positive M/EI diagram = area of negative M/EI diagram.

(b)       The second condition provides that the net moment of the  M/EI diagram about the vertical through B is zero which means the moment of area of positive M/EI   diagram about B = moment of area of negative M/EI   diagram about B.

The fields of the diagrams and their CG distances from B are shown in Figures 13(d) and (e) from which we get:

(a) Pas/2EI +((M_A+M_B)/2EI)I = 0

(b)       (Pab/2EI) . (b+1/3) + ((M_A+M_B/2EI)l) . 2M_A+M_B/M_A+M_B .1/3 =0

that while simplified provides the following simultaneous equation

(M _A + M _B ) = - Pab/ l

And 2 M _A  + M _B = -  Pab (l + b)/l ²

Subtracting the first from the second

M _A = - Pab²/l²                                                                                                                                        

Substituting the value of MA in first equation above, we get

MB = -Pab/L -(-Pab²/L²)

=-Pabl/l²+Pab²/l²

=- Pab/l²(a+b-b)

=- Pa²b/l²                                                                                                                       

Here, because of their negative signs MA and MB are both hogging moments. But from the point of view of statics MA is an anticlockwise moment while MB is a clockwise moment as shown in the diagram.

Again by taking moments about B, we have

V_A l - Pab²/l² +Pa²b/l² -Pb =0

giving  V_A =Pb/l +Pab/l³ (b-a)

and V_B=Pa/l -Pab/l³ (b-a)

In Eq. (2.22), we clearly see that the first term in either case is the reactions of a simply supported beam; while the second term is caused due to the fixity of the supports. The sum of V_A + V_B remains equal to P for vertical equilibrium.

A maximum positive BM occurs below the load and is given by

M_C   = - M_A +V_A.a =2Pa²b²/l³.