Benefits of the symmetry of the structure:

We shall take benefits of the symmetry of the structure.

The fixed end moments MA and MB are both hogging (negative) and of equal value due to symmetry. On the left end hogging moment MA is anticlockwise; on the right hand end it is clockwise in direction. Due to the statical condition, ∑ H ≡ 0, the two horizontal reactions at HA and HB are both zero.

Because of symmetry both the vertical reactions V_A and V_B are equal and

V_A + V_B = wl ∴ V_A= V_B= wl /2.

Further, considering the beam as simply supported at A and B you know that the free beam BM diagram is parabola with maximum ordinate at centre equal to wl²/8 as shown in Figure.

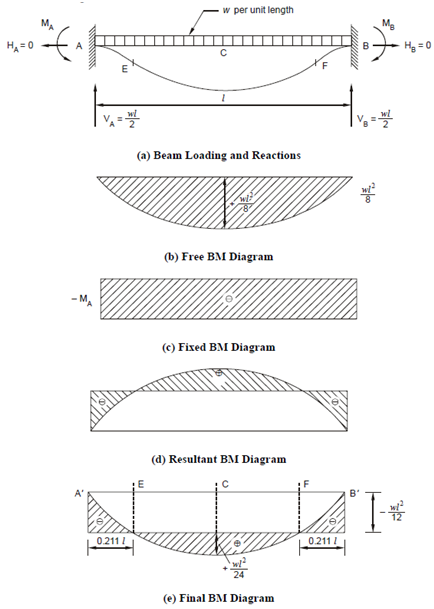
Because of fixed end moments the negative BM diagram will be a rectangle as both the end moments are equal and negative as shown in Figure (c).

The resultant bending moment diagram is obtained by superimposing Figure (c) on Figure (b) as shown in Figure (d). Now the value of the unknown moment - M_A is obtained by the compatibility condition that the change in slope from end A to end B is zero. (Because the beam is fixed at A and at B the slopes at both ends are zero.) By the first moment area theorem this is equal to the area of the M/EI   diagram between A and B, hence the net algebraic value of the M/EI diagram from end A to B is zero.

This implies that the area of the positive free M/EI diagram is equal to the negative M/EIdiagram. The EI is constant; M/EI   diagram will be similar to M-diagram. As area of the parabola is 2/3 ×  area of circumscribing rectangle, the area of the positive M/EI diagram is 2 /3× wl²/8EIx1 = wl³/12 EI.