Theorem of Three Moments:

this method, an equation is established relating the three support moments of any two adjacent spans of the continuous beam. Thus, a relation is established between the support moments M₂, M₃, M₄ (at support numbers 2, 3, 4) of the two adjacent spans L₂ and L₃ and so on. A continuous beam on n supports has (n - 1) spans. Thus, (n - 2) equations will be established. We also know that out of the n support moments, the two support moments at the ends are zero. Hence, the (n - 2) unknown intermediate support moments can be determined from the (n - 2) simultaneous equations. As the equation establishes a relation between any three consecutive support moments, it is called the equation of three moments. This will be explained now.

The basis of this equation is the compatibility condition which ensures the continuity of the beam between adjacent supports. Simply told this means that as the beam is continuous over the intermediate support the tangent to the elastic curve at the support is common to the adjacent spans and its slopes on the two sides are same. This is shown in Figure d).

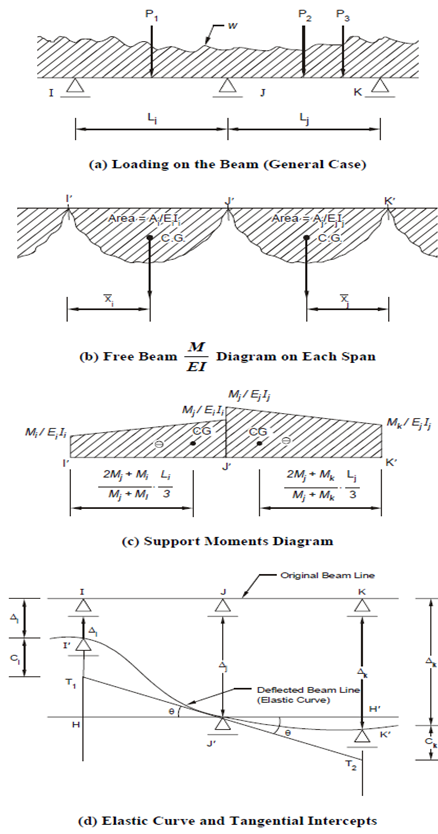
Figure 18(a) shows any two adjacent spans L_i, L_j of the continuous beam, and the loading diagram. The supports I, J, K sink by amounts Δ_i, Δ_j and Δk and the new elastic curve is shown in Figure (d). The tangent at the central support J ′ is T₁ J ′ T₂ which meets the verticals through I and K at T₁ and T₂ respectively.