Proof That Energy Is A Property

The figure illustrates a diagram with random properties of a system x and y as abscissa and ordinate. The points 1 and 2 symbolize two states of the system.

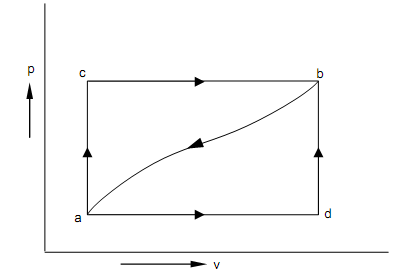
                     Figure: Path of two cyclic processes passing via two common state points

Let consider a cyclic process performed by the system. Beginning from state 1, the procedure proceeds to state 2 all along the path marked A, and returns to state 1 all along the path C. From First Law we can write:

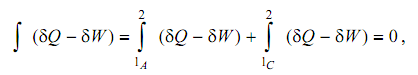
in which the summation around the cyclic procedure has been divide into its component parts. Let now consider a second cyclic process, that varies from the first in that the outward path is now B instead of A. Applying the First Law to this procedure, we acquire:

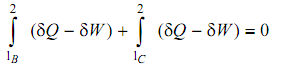
From examining the above two equations we see that

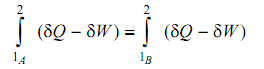
This illustrates that the integral of (δ Q - δ W) from state 1 to state 2 is similar for paths A and B. As these have been randomly selected, we say that the integral has similar value for any path between 1 and 2.

Representing ∫ δ Q by Q, the total heat transfer during the procedure from 1 to 2, and ∫ δ W by W, the total work during the similar change of state, we can say that (Q – W) has similar value for any path between 1 and 2. From the definition of energy, equation

                                                     Q – W = E₂ –E₁

therefore it is seen that (E₂ − E₁) has similar value for any path among 1 and 2. This entails that the value of (E₂ – E₁) based only on the end states. Now using properties of properties, it obeys that energy E is a property.