Risk and Return of a Portfolio:
We have been discussing the ex-ante and ex-post risk and return associated with a single stock. However, investors often hold a portfolio of assets. We shall be discussing the portfolio theory of asset pricing in greater detail in the next section. However, here we set out the basics of risk and return associated with a portfolio of assets. This type of analysis was pioneered by Harry Markowitz. Markowitz observed that investors do not always try to maximize returns. If they wanted to do so, they would simply hold only that security which they expected would give the highest returns. Thus investors are concerned both with return and risk, and since they hold a portfolio of assets, it showed that diversification can lower risk without adversely affecting returns.
The return for a portfolio is simply a weighted average of the returns of the securities in the portfolio. For a single time period t, the portfolio return is calculated as:
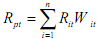
where Wit is the market value of the ith asset divided by he market value of the entire portfolio.
For ex-ante calculations:
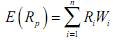
the variance of a portfolio is a little complicated because we also have to consider any two assets of a portfolio together. The general formula for variance of a portfolio is
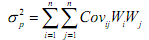
Where Covij represents the covariance between any two assets I and j. We can calculate the correlation coefficient
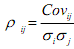
The correlation coefficient always lies between -1 and +1 and is a measure of the strength of the linear association between assets i and j. A value of -1 or +1 shows perfect linear relation (the former an inverse relation) while a value of 0 shows no relationship. You have studied about these concepts in the course on quantitative methods in the first year.