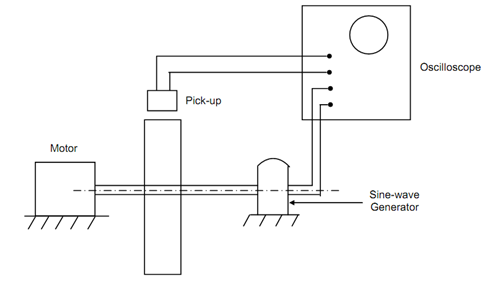
Balancing of a Thin Disc:

The class of rotors as industrial fan, wheel, blowers etc. may be considered as thin disc. A pick-up is utilized to measure oscillations of the thin disc in say vertical direction and the output is displayed on the double oscilloscope. A sine wave generator is associated to the disc and produced sine wave is fed to the second beam of the similar oscilloscope. The sine wave is utilized as a reference for measuring phase of the pick-up signal

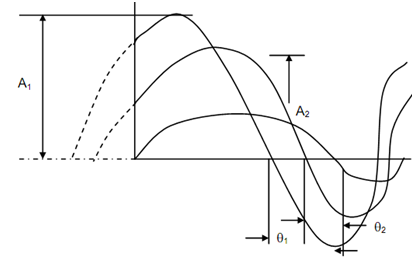
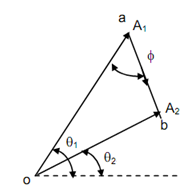
Primary the disc is rotated at a speed that is adequate to produce measurable amplitude of oscillation. Consider A₁ be the amplitude and θ₁ be the phase difference along reference to the sine wave. Next a trial mass 'mi' is associated to the disc at a known angular location and at a known radius. The disc is rotated at the similar speed. Consider the amplitude of this oscillation be A₂ and assume phase difference be θ₂. Now both of these vectors are plotted. Consider

A₁ be defined by and A₂ by  as illustrated in Figure 8(c). The vector  defines the effect of the trial mass 'mi'. Therefore, to nullify the effect of  a balancing mass m_b must be added at the similar radius as that of trial mass such that

m_b  = m _i  (oa/ ab)

at an angle φ clockwise in this case.

 (i)

    (ii)

     (iii)

If a phase meter is employed the utilization of sine wave generator may be avoided. In the field balancing measurement of phase might be hard. In that case, the following four readings might be taken for vibration amplitude

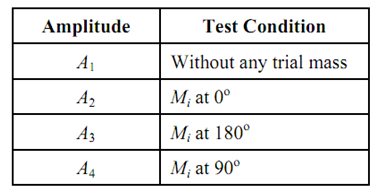
When taking these runs along trial mass (less three runs) the radial distance of the trial mass must be kept similar.

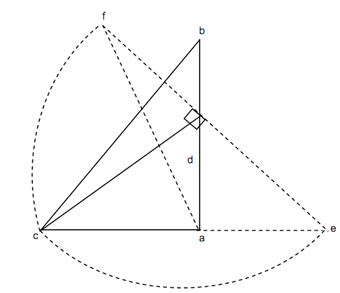
Draw a triangle 'abc' by taking ab = 2A, ac = A₂ and bc = A₃ as illustrated in Figure 9. Consider 'd' be the middle pt of ab. The magnitude of the balancing mass is specified by

mb  = m (ad / dc) and angle φ =∠ adc

If magnitude of A₄ is given by ac, the angle must be calculated counter clockwise. If magnitude of A₄ is given by af, angle φ must be measure in clockwise sense.