Determination of Fatigue Strength

Staircase testing of material for determination of fatigue strength or limit is very popular and is illustrated in Figure 1.40. A stress level σ0 is approximately determined to be in the vicinity of fatigue strength, σe (for performing an experiment σ0 may be taken as half of ultimate tensile strength). Then a fixed stress step d0 is chosen so that,

                                   σ1  = σ0  + d0 , σ2  = σ0  + 2d0 , σ3  = σ0  − d0  etc.

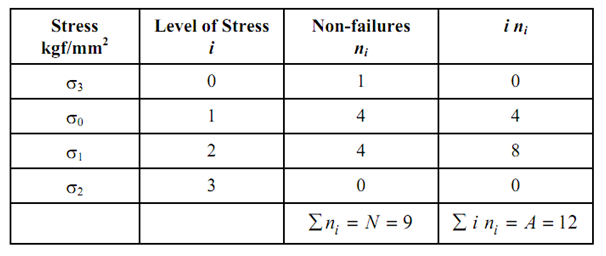
A number of identical specimens are first chosen (between 15 and 20 specimens) and one is loaded in the machine at stress level σ0. If this specimen survives the specified number of cycles (commonly 107 cycles), the next specimen is tested at σ1, if this survives 107 cycles, the next specimen is tested at σ2. A failure at this level is followed by testing at σ1 and so on. The failures and survivals are plotted as × and 0 against each stress level in Figure 40. Table 3 describes the method of calculation of fatigue strength.

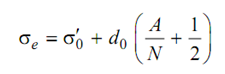
                                                                   A = ∑ i ni
                                                                   N = ∑ ni

where i denotes the level of stress as 0, 1, 2 etc.   is the stress level which is lower and at which a non-failure is obtained. It can be seen from Table 3 that σ3 is the stress level at which no failure is obtained. Apparently σ3 is the lowest stress, which is equal to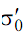

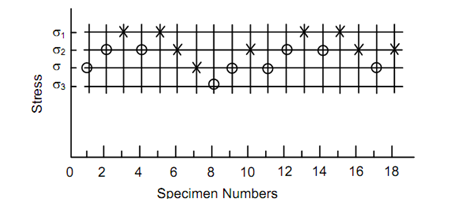
                           Figure: Staircase Testing Sequence and Failure Survival Pattern

                                                    Table: Analysis of Staircase Data

From Eq. (1.22) and Table 1.3, fatigue strength,

σ e = σ3  + d0   ((12/9)  + (½)

If, for example,

σ3  = 280 N/mm²  and d0  = 5 N/mm²
σe  = 289 N/mm²