Mapping of WFPR into AFPN

A knowledge based systems can be modelled as an Adaptive Fuzzy Petri Nets via mapping its Weighted Adaptive Fuzzy Petri Nets into small Adaptive Fuzzy Petri Nets and then combining them into ordinary places. In order to map Weighted Fuzzy Production Rules to Adaptive Fuzzy Petri Nets, we follow following process:

(a)   Map propositions as places.

(b) The connection THEN between the consequent and antecedent proposition like arcs and transitions for composed disjunctive rules more transitions are required.

(c) The antecedent proposition's weight and certainty factor of the rule like the weights of the output and input arc of the consequent transition, respectively.

Here, mapping the three types of weighted fuzzy production rules into the Fuzzy Petri Nets is given step by step as specified below:

(a)   A simple fuzzy production rule as in Type 1 discussed above

R: IF a THEN c, λ, w (CF = μ)

Rule R is shown in terms of Fuzzy Petri Nets as given in following figure.

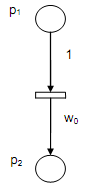
                                            Figure: Mapping of WFPRs into AFPNs as in Type 1

(a)   A composed conjunctive rule as in Type 2

R: IF a₁ AND a₂ AND...AND an THEN c, λ₁, λ₂, . . . , λ_n, w₁, w₂,..., w₃

(CF = μ).

Rule R is presents in terms of Fuzzy Petri Nets by following figure.

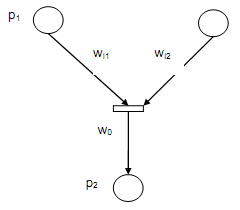
                                               Figure: Mapping of WFPRs into AFPNs as in Type 2

(a)   A composed disjunctive rule as in Type 3

R: IF a₁ OR a₂ OR...OR an THEN c, λ₁, λ₂, . . . , λ_n, w₁, w₂, . . . , w₃

(CF = μ).

The rule R is shown in terms of Fuzzy Petri Nets by following figure.

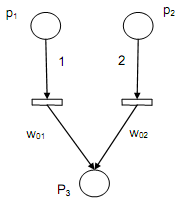
                                                Figure: Mapping of WFPRs into AFPNs as in Type 3