Implementation of AFPNs

After an Adaptive Fuzzy Petri Nets has been implemented, this can be employed as an inference engine. The implementation of an inference engine is realized by firing transitions. Any type of transition fires as quickly as it is enabled and a transition t is considered to be enables if all the input places have tokens that certainty factors are greater than their thresholds.

See the following:

Suppose that I (t ) = { p_i1 , p_i2 , . . . , p_in } and the subsequent input weights are specified via, Weights : w_I1 , w_I2 , ... , w_In . Equally the consequent thresholds are specified by,

Thresholds λ₁, λ₂, ... , λ_n

Here, for all t ∈ T, t is enabled and fired if for all p_ij ∈ I (t ) , the certainty value α ( p_ij ) ≥ λ_i , j = 1, 2, ... , n holds. Subsequent to firing t, the token in p_ij is removed, and a token along with certainty factor w_Ok  × (min λ_ij  + ∑ (α ( p_ij ) - λ_j ) × w_ij ) is put into all of its output places p_ok, k = 1, 2, ... , m . The new certainty factor of p_ok is the innovative token that is generated by the transition along with the maximum output weight, if a place p_ok has more than one input transitions and more than one of its input transitions fire.

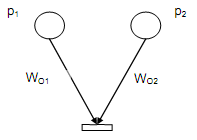
                          Figure: A Part of a Petri Net Model showing more than 2 Input Transitions to a Place