Machine Table Tour Planning

The last matter to be addressed in the fulfillment of the second insertion planning criterion such is to minimize insertion bed tour. To that end, the sequencing methodology applies the guidelines detailed via Rule 4. This rule such applies to the insertion of components of the same shape, size, and electrical values, aims at choosing the component insertion sequence that results in the shortest machine table movement.

This problem has historically been treated like a traveling salesman problem. The traveling salesman problem can be stated as given: given a group of cities to be visited along with known distance among any two of them, get the shortest route to visit each city once and return to the starting point.

This has been proved that for a problem including n cities, the number of possible round trips is as n-1! 29. If n = 50, then there would be 3.083 × 1062 possible tours. Since such an exhaustive search is generally unfeasible for most practical reasons, heuristic methods have been applied to get solutions to this kind of problem such could be considered as acceptable if not optimal.

There are some solution methodologies to this problem, as like: the bound and branch method, clustering methods, and the nearest neighbor algorithms. Among them, the nearest neighbor method is the most widely utlized heuristic in industry and therefore the one that was applied in this illustration.

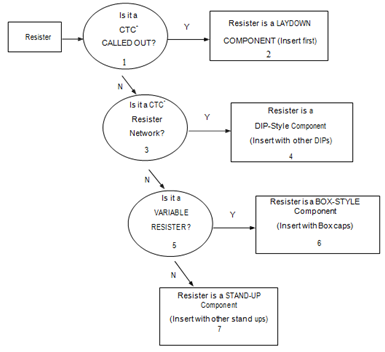
                                                                 Diagram of: Resister Sequencing Decision Tree