vNM Expected utility theory:

von  Neumann and Morgenstern showed  that under  the assumptions of rationality, continuity and independence, it  is possible to choose a particular- utility  function  u, which represents the preferences and has  an expected utility form:  

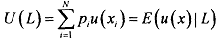
Take note of  the notation we  are using  in  the discussion. The lower  case  u , defined over  states, is called Bernoulli utility function while  the upper case IJ,  defined  over  lotteries, is  known  as  von  Neumann-Morgenstern  (vNM) utility  function. We will  overlook  the  difference of  usage  here and call  the utility formulation as vNM expected utility function. The utility  function  u  over  states  uniquely  defines the  preferences of  an individual  over the  larger domain  of  the  lotteries.  It  carries  a lot  more information  than an  arbitrary utility function over X. A monotonic transformation may, actually, distort some of this information. However, if the two utility functions are linear monotonic transformations of one another, and we can write then they represent the same preferences over uncertainty.

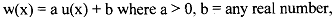
When we discuss the utility of a lottery in vNM expected utility form, we are essentially considering  the expected utilities  u,  of the N outcomes. 'l'hat  is to say, a utility function that has expected  utility property must have  the  feature that the utility of a lottery is simply the (probability) weighted average of the utility of each outcome, viz.,