Expected utility theory and risk aversion:

Let us  extend  the discussion of expected utility preferences to  link with  risk aversion. Note that ordinarily people dislike risk. Therefore, we can ask, how much a consumer would be willing  to pay  to avoid a  fair  bet. A fair oet  is a lottery whose expected payoff is equal  to zero. With such payoff, you  either gain or lose money by playing them. That means, such lotteries expose you to risk, and we are trying to measure the aversion to such types of risk. We conceive of concavity or convexity form of a vNM utility function where properties that  are  not generally preserved  by  arbitrary monotonic transformation.  Then  it  will  be possible to see that they  cany  a  lot  of information about individual attitude  to  risk.  You  can consider Jensen's inequality for that purpose which tells us that for any concave u  ,  

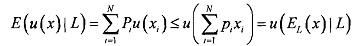
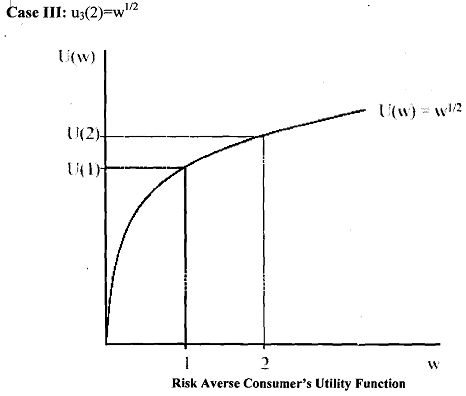
That  is, an individual, whose preferences are represented by  a concave utility function prefers to have the amount of money  equal to the expected value of the  lottery  to having the lottery itself. Such an  individual  is known as risk- averse individual.

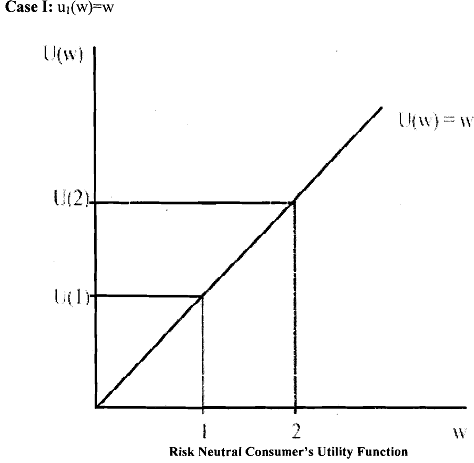
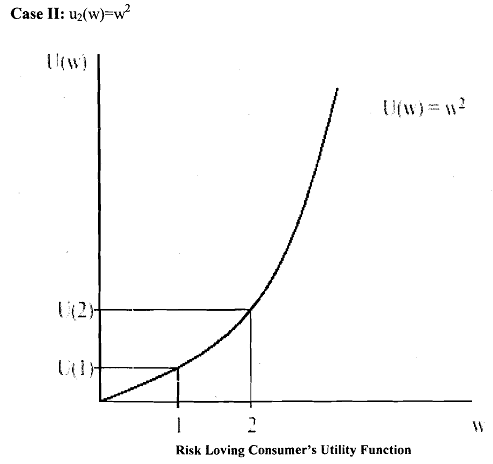
The above inequality  is  reversed for convex  u  and  the  individual will  be called  risk-loving  individual.  Finally, when  u  is  linear,  (i.e., u(x)=x),individual will consider only  about  the expected value of the lottery and will be  indifferent to risk. In such a situation, she will be known as risk- neutral  individual.

Consider  the  following three utility functions  (due to  Autor,  2004) characterising three different expected utility maximiser: