Risk aversion and insurance:

We  have drawn mostly  from  Autor, 2004  for  developing  this  section. Consider insurance that  is actuarially fair, meaning that the premium  is equal to expected claims: Premium =  (pA) where p is the expected probability of a claim, and A is the amount of the claim in even of an accident.

We  start with a risk-averse person's  decision  to buy  insurance by taking  the initial endowment wealth  wo,  where  L  is  the amount  of  the loss  from an accident  

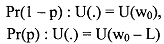
If insured, the endowment is (incorporation  the premium PA, the claim paid A if a claim is made, and the loss L):

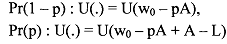
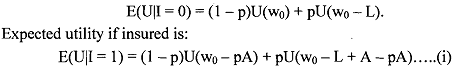
We need to find out the amount of insurance that should be bought. See that the insurance can be bought they could buy upto their total wealth: wo - pL.  To  solve for  the  optimal  policy  that  the agent should  purchase, differentiate (i) with respect to A:

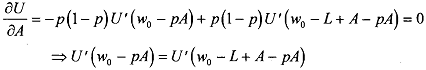
=> A = L, which  implies that wealth  is w_o  - L in both  states of the world (insurance claim or no claim) Thus, a risk averse person will optimally buy  full insurance if the insurance  is actuarially fair. You can verify that for this kind of a consumer the expected utility  rises with  the  purchase of  insurance although  expected wealth  is unchanged.

Next, let us solve for how much the consumer would be willing to pay  for a given insurance policy. Since insurance increases the consumer's welfare, she would be willing to pay  some positive price  in excess of  the actuarially fair premium to defray risk. Thus, the agent is trying to equate the marginal utility of wealth  across states. Because, the utility of average wealth  is greater than the average utility of wealth for a risk averse agent.

The agent wants to distribute wealth evenly across states of the world, rather than concentrate wealth in one state. She will attempt to maintain wealth at the same level  in all states of the world, assuming that she can costlessly transfer wealth  between states of  the world  (which  is what  actuarially fair  insurance allows the agent  to do).

The above formulation of insurance problem  is exactly analogous to  convex indifference curves over consumption bundles. It can be seen that diminishing marginal  rate of substitution across goods, which comes from diminishing marginal utility of consumption, causes consumer's to diversify across gods rather  than specialize  in  single good; and diminishing marginal utility  of wealth causes consumers to wish to diversify wealth across possible states of the world rather than concentrate it in one state. The insurance problem would change if the consumer were risk  loving. Such an individual would  like to be at a comer solution where all risk is transferred to the least probable state the worlci, again holding constant expected wealth.