Certainty Equivalent:

A consumer faces a lottery with 50/50 odds of either receiving two rupees or nothing, so that the expected monetary value of this lottery is R. We will show that these three consumers differ in risk preference. First, notice that  u₁(1) = u₂(1) = u₃(1) = 1. That  is,  they  all value one rupee with certainty equally. Consider the Certainty Equivalent  for a  lottery E that is a 50/50 gamble over Rs.2 versus 0. The certainty equivalent is the amount of cash that the consumer  is willing to accept with certainty in lieu of  facing lottery E.

The expected utility value as  depicted in the above figures are:  

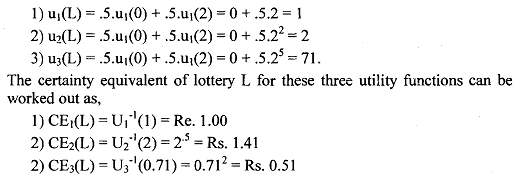
Thus, depending on the utility function, a person would pay Re. 1, Re.  1.4  1, or Rs.0.51 to participate in this lottery. Although the expected monetary value E(V) of the lottery is Rs.1.00, the three utility functions value it differently:

1)  The person with U1  is risk  neutral: CE = Re  1.00 = E(Va1ue)  =>  Risk neutral

2)  The person with U2 is risk loving: CE = Rs.  1.41  >  E(Va1ue) =>  Risk loving

3)  The person with U3 is risk averse: CE = Rs. 0.50  < E(Va1ue) =>  Risk averse.

The  risk preference  is  decided  by  the  concavity or convexity of  the  utility function. So we can write expected utility of wealth:

and an important result of expected utility  theory  can be obtained for a  risk averse agent which  states,  given non-zero risk, the expected utility of wealth is less than the utility of expected wealth.

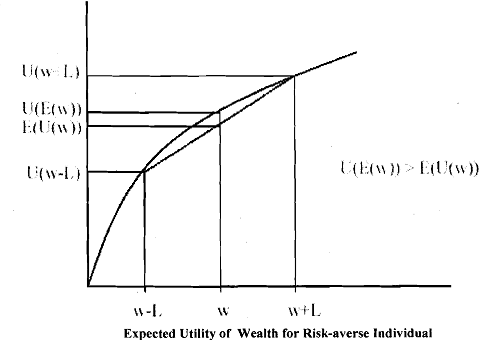
The reason is, if wealth has diminishing marginal utility, which is true if U(w) = w^1/2,  losses in terms of the cost of utility are more than equivalent monetary gains.Consequently, a risk averse agent is better off to receive a given amount of wealth with certainty than the same amount of expected wealth.