Newton's Divided Difference Method:

In this, the n^th order polynomial is taken as

y = a₀ + a₁ (x - x₀) + a₂ (x - x₀) (x - x₁) + . . . + a_n (x - x₀) (x - x₁) . . . (x - x_n - 1) A recursive formula is written down to find out the coefficients. The higher order coefficients are found out from the lower order ones. The coefficients are appraise beginning with a₁, a₂ and a₃ and so on up to a_n.

The general form of the n^th order Newton's polynomial might be written like

y = c₀ + c₁ (x - x₀) + c₂ (x - x₀) (x - x₁) + . . . + c_n (x - x₀) (x - x₁) . . . (x - x_n - 1)

To determine the (n + 1) coefficients, we require n + 1 data points such as (x₀, y₀),

(x₁, y₁) . . . ( x_n, y_n).

The coefficients are specified by

c₀ = y₀

:

:

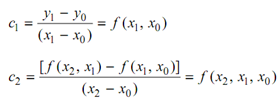
c_n  = f ( x_n , x_n -1, . . . , x₁, x₀ )