Higher Degree Polynomials:

Let the general form for a polynomial of order n.

f (x) = a₀ + a₁ x + a₂ x₂ + . . . + a_n x_n

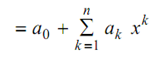
The solution for this set of n + 1 constants a₀, a₁,--------- an, we need n + 1 simultaneous equations and we want n + 1 data points. By using least square approach and Gaussian elimination technique the best fit polynomial might be evaluated.

                                                    X = A^{- 1} B

Already we know how to solve out this problem. Remember Gaussian elimination?

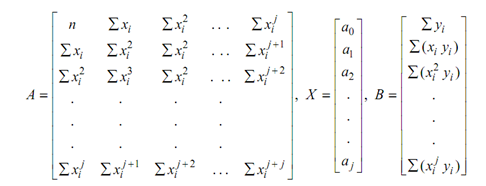
Here all summations are over i = 1, . . . , n data points.