The Marginal Effects in the Logit Model:

As  mentioned  earlier the  logit model is  computationally more  tractable  than  the probit model. The cumulative distribution function admits of a closed form (integral free). Consequently the expressions for the marginal effects are straightforward and easy  to  interpret. we  deduce that the odds ratio for the logit model  is

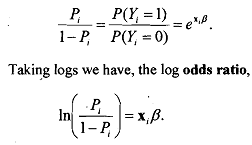
This is a linear function of the parameter vector 8. This makes  the  analogy with standard linear regression easier  to comprehend. Differentiating gives us

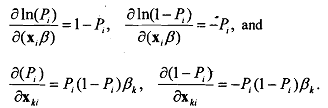
We  could also have obtained these expressions directly by substitution for f(.) . Remember that Y,  is a Bernoulli variable and V(Y_i) = P_i(l-  P_i). Therefore, the impact of a small change in  the k^th  independent variable on the probability of the individual  joining the'labor force is given by  the variance of Y,  times the coefficient β.  The variance term on the right hand side of the expressions  in  captures the uncertainty arising from the lack of information on Y.