Interpretation of coefficient:

As  in  any nonlinear regression model the parameters of the  logit and probit models, are not  necessarily  the marginal  effects. This is  in  contrast to 'the interpretation of parameters  in  linear models we are accustomed to analyzing. The data available  in these models  is  "limited",  that  is,hhe  information available to us  is  less than  in  a. standard regression model. Therefore, we can no longer ask and answer the usual set - of quistions. All questions and answers now pertain not to the dependent.variable Y (or Y*)  but to  the probability of Y taking the value one or zero. In general,

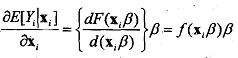
where A.)  is  the probability density function that corresponds to  the (cumulative) distribution  function, F(.).

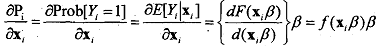
While computing marginal  effects, for making  inferences,  the  expressions can  be evaluated at the sample means of the data or evaluated at every observation and then averaged. The latter practice is favored by most researchers (provided the necessary regularity conditions are satisfied). Note also that the same scale factor applies  to all the slopes in the model.

In addition,'  one must be careful while computing  the impact of dummy, independent variables on  the probability of choice. The  derivative  is  with  respect  to  a  small change, and it is not appropriate  to apply for the effect of a change in a dummy variable. The correct marginal effect for a dummy independent  variable, say d, would be given by:

Prob[Y = 1] d = 1,  means of all other  independent variables]  - Prob [ Y = 1]  d = 0, means of all otiiir independent variables]
The expressions obtained above are considerably simplified in  the case of the logit model.