Hypothesis Testing and Goodness of Fit:

For  testing hypotheses about  the  coefficients,  all  usual procedures  are  available. Tests  on  an  individual  coefficient will  be  based  on  the  usual  t  tests,  using  the standard errors from  the  information matrix.  The Wald  test can be  used  to test a hypothesis about a subset of coefficients. Likelihood ratio and Lagrange multiplier statistics can also be computed. One of these procedures can also be used  to test for heteroscedasticity or omitted variables. These tests are important as existing  research indicates that  the  probit  and  logit  models  are  not  robust  to the  presence  of heteroscedasticity or the omission of variables.

Several different measures have been  suggested. The important  thing to remember is that we are looking for a measure of how well the model approximates  the obsewed data. The dependent variable being qualitative  and binary, accuracy can be  judged by looking at how well the calculated probabilities and the observed frequencies  tally or by  how well the model predicts observed responses.

Several measures analogous to the R² measure for  linear regression have also been proposed. McFadden has proposed the likelihood ratio index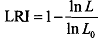

The measure is bounded between 0  and  1.  If all the slope coefficients are zero then LRI equals zero. However, the LIU never attains  the value 1.

Another popular  tool available to  us  (one  that should be  used with  caution)  is to summarize the predictive ability of the model by  forming a 2 x 2 table of the hits and misses of a simple prediction rule such as

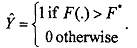
Usually F*  is set equal to 0.5 or slightly higher. However,  it  is possible to.construct examples which make  it  clear  that  this tool is useful as a starting point but is not always accurate  in evaluating models.