Test of measurement errors:
Suppose we are estimating the two-variable regression model
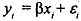
There is a possibility that x might be measured with error.
If 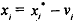 then the actual least squares regression would be
then the actual least squares regression would be
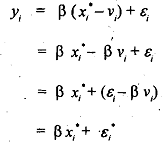
Where 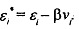
If x is measured with error, we have seen that consisent estimator of x* can be obtained by using an instrument z which is correlated with x* but uncorrelated with E and v Suppose the relationship between z and x* is given by
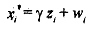
When (9.18) is estimated using least squares, we obtain
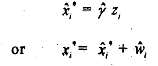
where G, are the regressioll residuals. Substituting the value of eq. (9.19) into eq (9. i 7) we have
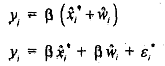
Whether or not there is meftsmsnt error, the coefficient of ite will be consistently estimated by ordinary lawt squares, since
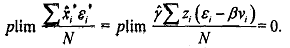
In fact, the least-squares estimator of the coefficient of x* in eq. (9.20) is identically equal to the instrumental-variables estimator, which is given by
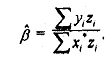
To look at the coefficient of the variable  , note that
, note that
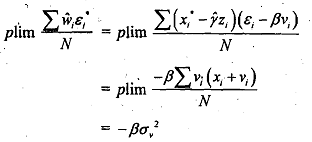
When there is no meburernent error, σv2 = 0, so that OLS applied to eq. (9.20) will generate a consistent estimator of the coefficient of . However, when there is measurement error, the coefficient  will be estimated inconsistently. ' This suggests a relatively easy measurement error test. Let δ represent the coefficient of the variable I?, in eq. (9.20).
will be estimated inconsistently. ' This suggests a relatively easy measurement error test. Let δ represent the coefficient of the variable I?, in eq. (9.20).
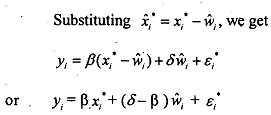
With no measurement error, δ= β, so that the coefficient of 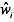 , should equal zero. However, with measurement error, δ ≠ β, and the coefficient will (in general) be different from zero. We can test for measurement error by doing a simde two-stage procedure. First, we regress x* on z to obtain the residuals
, should equal zero. However, with measurement error, δ ≠ β, and the coefficient will (in general) be different from zero. We can test for measurement error by doing a simde two-stage procedure. First, we regress x* on z to obtain the residuals 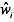 . Then, we regress y on x* and
. Then, we regress y on x* and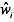 , and perform a t test on the coefficient of the ii, variable. If we are concerned with measurement error in more than one variable of a multiple regression model, &I equivalent F test could be applied.
, and perform a t test on the coefficient of the ii, variable. If we are concerned with measurement error in more than one variable of a multiple regression model, &I equivalent F test could be applied.
The test just described is a special case of a more general test for specification error proposed by Hausman. The Hausman specification test relies on the fact that under the null hypothesis the ordinary least-squares estimator of the parameters of the original eq. (9.17) is consistent and (for large samples) eRcient, but is inconsistent if the alternative hypothesis is true.
However, the instrumental-variables estimator [the least-squares estimator of eq. (9.20)] is consistent whether or not the null hypothesis is true, although it is inefficient if the null hypothesis is not valid. The Hausman specification test is as follows: If there are two estimators β1, and β2 that converge to the true value p under the null but converge to different values under the alternative, the null hypothesis can be verified by testing whether the probability limit of the difference of the two estimators is zero.