Inverse regression:

When we have  the variables  y andx  both measured with errors (the observed values being y* and x'),  we consrider  two regreesion equations:

1)  .Regression  of  y'  an  x',  which is called the "direct"  regression.

2)  Regression of x'on y', which is called the "inverse" or "reverse"  regression.

Inverse regression bas beep frequently advocated in the case of analysis'of salary discrimination.  Since  the problem  is one of usual errors  in variables, both regressions need  to  be computed and whether inverse  regression alone  gives the correct estimates depends on the assumptions we make.

The usual model, in its simplest form, is  that of two explanatory variables, one of which is measured with error  

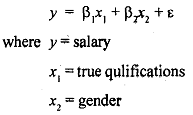
What we are  interested  in is  the coefficient  of x₂. The problem is that x_i  is measured with error.

Then β₂ >  0  implies  that men are  paid more  than womenwth  the same qualifications and  thus  there is gender  discrimination  A  direct least squares estimation  of eq. (9.22) with x,' substituted for  x,,  and β₂ >  0  has been frequently  used as widen& of gender discrimination.

In the inverse regression wg  take

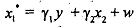
We are asking  whether mep w  mor<or  less qualified  than women ha3ing  thesame salaries. The  proponents of inverse  regression argue  that  ta establish discrlimation, one has  to have y₂<  0  in eq. that  is, among men and women receiving  equal salaries, men possess lower qualifications.

The usual errors  in variables  results however show that we  shauld nat make inferences on the basis of β₂, and y₂ but obtain bounds for β₂,  from the direct regression and the inverse regression estimates.