Instrumental variables method:

The problem of errors  in the measurement of variables  in regression models  is quite important, yet econometricians do not have much to offer in the way of useful solutions.  As a general rule, we tend to pass over  the problem of measurement error, hoping that the errors are small enough which will not destroy the validity of the estimation procedure. One  technique which  is available and can  solve the measurement error problem is the technique of instrumental variablys estimation.

We briefly outline  the concept of instrumental variables because it is likely to be useful with measurement errors.  

The method of instrumental variables involves  the search  for a new variable Z which is  highly correlated with  the independent   variable X and at  the same time uncorrelated with the error tern in the equations well, as the errors of measurement of both variables).  In practice, we are conceined , i^th  the consistency  of parameter estimates and therefore concentrate on the relationship between the variable Z  and the remaining variables in the model when the sample size gets large. We define the
random variable Z  to be an instrument . if the following conditions  are met.

1)  The correlations  between Z and ε,  u, and v, respectively,  in the regression approach zero, as the sample size gets large.

2)  The correlation  bet&een Z and X is nonzero. as  the sarnde  size gets large.

We simply select  one  instrument (or combination of  instruments) that has  the highest correlation with the X  variable.

Assuming for the moment  that such a variable can be found, we can alter  the lewt squares regression procedure to obtain estimated parameters that are consistent.

Unfortunately,  there is no guarantee  that  the estimation process will yield unbiased parameter  estimates.  To simpli@the  matter, let us consider  the case of measurement krrors  in  the  independelt  variable such that y_i = βx_i + ε_i only x ismeasured with error (as x*= x + v).  In order  to solve the problem we take the regression equation y_i = pz_i +  Where Z  is the  instrumental variable.  The  instrumental variables  estimator of the regression slope  in the above model is

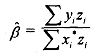
The choice of this particular slope formula is made so that the resulting estimator will  be  consistent. To  see this, we can  derive the relationship between  the instrumental-variables  estimator  and the true slope parameter as follows:

Clearly, the choice of Z as  an instrument guarantees  that  will approach β as the sample size gets large [Cov (z, E*)  approaches O]  and will therefore be a consistent estimator  of β. Remember that the variable x,'  in (9.16) was not replaced by z,  in the denominator of instrumental variables estimator, as the estimator  does 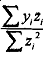not yield a consistent estimator of P. Let us show this.

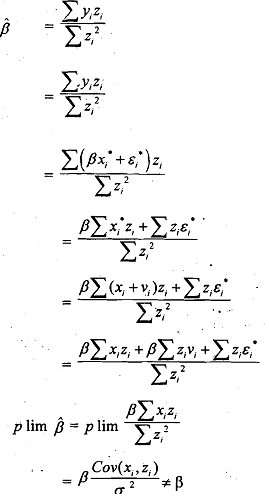
The above shows  that 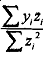will not yield a consistent estimator of β.

The technique of instrumental variables appears to provide a simple solution to a difficult  problem. We have defined an estimation  technique, which yields consistent estimates  if we can  find an  appropriate instrument.

A few  concluding comments may be instructive.

i)  First, the OLS.  estimation technique is actually a special case of instrumental variables.: This follows because  in  the classical regression model X  is uncorrelated with the error  term and because  Xis  perfectly correlated with itself.

ii)  Secorid,  if we generalize the measurement error  problem  to errors  in more  than one independent variable, one instrument is needed to replace each of the designated independent variables.

iii)  Finally, we repeat that  instrumental-vdables  estimation guarantees consistent estimation but does not guarantee unbiased estimation.