From the observations made above, it could be seen that if a smaller land area is being surveyed and plotted along with scale factor 'n' of smaller magnitude, the error because of inaccurate centering of table will be more critical, the significance factor gradually decreasing along with larger and larger values of n.

Inaccurate Centering

The position of instrumentation station on map shall be exactly over the station on ground it represents. The significance of accurate centering can be best emphasized through explaining the nature and impact of error on survey accuracy.

Let OG be the instrument station over that the instrument is needed to be set up and OP its plotted position on map plan as display in Figure . AOGB is the desired angle to be plotted, although AOPB is corresponding angle acquired by drawing rays AOP and BOP along with alidade centered at OP.

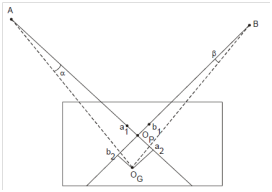
                                       Figure : Effect of Inaccurate Centering

The angular difference (∠ AOGB - ∠ AOPB) represents the error introduced because of inaccurate centering. A magnitude of error will be inversely proportional to the distance of reference stations A and B from instrument station OG. Instead of OG and OP being coincident, an angle α (= ∠ OG AOP) is introduced and hence similarity an angle β (= ∠ ΟG BOP) for station B. Let us also draw perpendiculars from O_G on ray OP B at b₂ and on ray OP A at a₂.

It can then be observed that

sin α = O_G a₂/O_G A

or, α= sin ^-1  (O_G a₂/ O_G A)

and sin β= O_Gb₂/ O_G B

or,  β= sin ^-1  O_Gb₂/O_G B

The angular error ∠ ΑΟGB - ∠ ΑΟPB would be equivalent to α + β. It can also be observed in which the position of A on the map marked as a1 is not accurate. It will be a few positions 'a' on the map left of a₁. Same, the true position of B on the map represented through 'b' will be on the right of plotted position b₁. Here the deviations of positions of A and B would be a1 a = α • a₁ a₂ and b1 b = β • b₁ b₂ correspondingly. These errors will depend on the scale of map chosen. Therefore, if scale selection is 1 cm on scale = n meters on ground, the plotted length OP a₁= (A O_G/n )cm

and     Op b₁= (BO_G/n) cms

Actual distance aa₁  =   AOG/n ×α cm = e₁ (say),

And bb₁  = BO_G/n ×β cm    = e₂ (say).

Commonly, during ploting, the maximum accuracy of plotting that can be achieved through even an experienced surveyor could be ¼ of a millimeter, i.e. (1/40) cm; thus deviation aa₁ or bb₁ which could cause error in plotting would be noticeable only while it is equal to or more than (1/40) cm.

Therefore, minimum value of e/n to be noticed will be 1/40.

or        e=  n/40

Alternatively, 'e' must not exceed n/40.

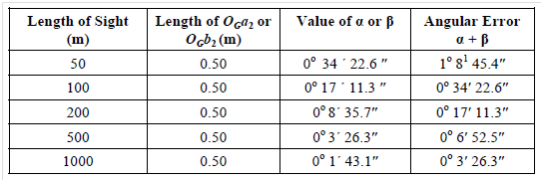
It could also be observed that normal size of the plane table is such in which maximum area on drawing sheet used for plotting could be 100 cm × 60 cm. Therefore, in common, the perpendiculars OB_Ga₂ and O_Gb₂ cannot exceed 50 cm in x-direction and 30 cm in y-direction. From this, a table could be prepared for different length of sights to take an idea of angular error which could be introduced because of inaccurate centering.