Forces and Stresses in Beams:
In other terms, the BM is called to be positive, at a section while it is working in an anticlockwise direction to the left & clockwise direction to the right of the section. The BM is called to be negative, at a section, when it is working in clockwise direction to the left and an anticlockwise direction to the right of the section.
Relation between Loading, Shear Force and Bending Moment
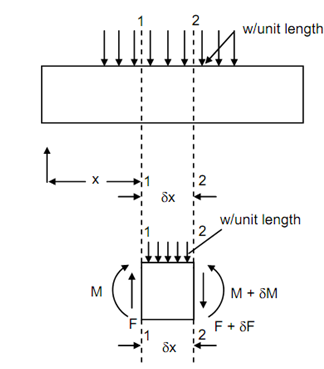
Let a beam subjected to external loading of intensity w per unit length. Let a small part of the beam between sections 1-1 & 2-2, δx apart, at a distance x from the left end support as illustrated in Figure. The load working on the small part is equal to w δx.
Let F & M be the SF & BM at left end to the element and F + δF and M + δM be the
SF & BM at right end of the element.
The forces & moments working on the element of the beam are as follows :
1. upward force F at section 1-1,
2. downward force F + δF at section 2-2,
3. downward load w δx,
4. anticlockwise moment M at section 1-1,
5. Clockwise moment M + δM at section 2-2.
As the element of the beam is in equilibrium, thus the system of forces & moments working on the element, should obey the laws of equilibrium. Now equating the unbalanced vertical force at section 2-2, we achieved
F + δF = F - w δx
Or δF / δx = - w ------------ (i)
Therefore, the rate of change of shear force (or in other terms, the slope of shear force curve) is equal to the intensity of the loading.
Figure
By taking moments around the section 2-2,
M + δM = M + Fδx - w(δx)2/2
Avoiding higher powers of small quantities & simplifying the relation, we obtain
M + δM = M + Fδx
or δM/ δx = F ---------- (ii)
Therefore, the rate of change of bending moment (or in other terms, the slope of the bending moment curve) is equal to the shear force at the section.
It is apparent that SF curve might be obtained by integrating the loading curve & BM curve may be obtained by integrating the SF curve.