Non-cyclic Power Plants

Both reciprocating IC engine and open-circuit gas turbine plant are non-cyclic, steady-flow, open-circuit, work-producing devices, that exchange heat with only one reservoir, namely, the atmosphere, and cannot be grouped as heat engines, engineers have selected in the past to compute the performance of such non-cyclic devices with reference to cyclic devices that are comparable in some limited respects, though this is not a rational process.

For the reason of stating a criterion of performance, it is supposed that the reactants move into the plant at the pressure and temperature of the atmosphere. When discharged back into the atmosphere, the exhaust products from real IC engine are very much hotter than the ambient temperature; there is hence a lost opportunity for generating work. The maximum quantity of work hypothetically accessible from a given chemical reaction is W_rev = − Δ G_o here Δ G is the difference in Gibbs function among products and reactants, and the subscript o refers to the state of the atmosphere. Then Wrev will be rational criterion against which to judge the work output of the real IC engine. Therefore, a rational measure of the fineness of performance for non-cyclic power plants will be the ratio of the real work output W to Wrev. This is at times termed as the rational (or energetic or Gibbs) efficiency as follows:

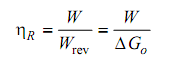
Dissimilar the thermal efficiency of a cyclic machine, the upper limit to this rational efficiency is observed to be 100%, the real value for an IC engine, whether turbine or reciprocating, is fine below 100%, and generally of much similar order as the thermal efficiency as high as 90% at light current. Loading and around 50% at helpful current loadings.

The quantity – Δ G_o for a chemical reaction can’t be established as readily as the calorific value, – Δ H_C; for this purpose the engineers have found small use for ηR. Rather they select to employ a purely random performance parameter by comparing the precise work output with the calorific value of the fuel. This might be termed as, at best, an arbitrary total efficiency.

Whereas for a heat engine, ηcy and ηH provide a direct connection among the work output of the cyclic plant and the calorific value in the non-cyclic IC plant. The engineer’s employ of the random overall efficiency is therefore completely arbitrary, when convenient, process. This must not be termed as the ‘thermal efficiency’ of the plant.

Then why does not the engineer run into problem with his employ of the random overall efficiency rather of ηR? This is mostly due to two factors:

• The associatively bad performance of the practical IC plant as compared to the ideal plant, and

• The fact which the difference among – Δ H_c and – Δ G_o is often small; this difference is specified by:

                                                          -G_O = - Δ H_c – T_o ΔS_o

Here Δ S is the entropy difference among products and reactants, and T₀ Δ S₀ is the heat transferred to the atmosphere in the ideal, reversible, work-producing procedure. This is positive for few reactions and negative for other, and is generally small as compared with the calorific value.

Despite the fact that IC plant are not cyclic work-producing machines, the values for the randomly defined total efficiencies for open-circuit gas turbine and reciprocating IC plants are of similar order as the rationally stated total efficiency of cyclic, closed-circuit gas turbine plant. Haywood advances the qualitative explanation for this: even whenever the IC plant employs little or no excess air, as in SI engine, 77% of the air employed is nitrogen, and it would make no difference to the operation of the plant when this N2 were regarded as being taken via a thermodynamic cycle. When, as in a gas turbine plant, 300% excess air were employed, no less than 94% of the air would stay unchanged in chemical composition in passing via the plant. Therefore, the relation among the work output and the calorific value in IC plant might be expected to be fairly similar to that in a cyclic plant working under comparable circumstances. This argument might therefore be provided to support the process of computing the cycle efficiency of a comparable cyclic plant by using air as the working fluid and containing similar compression ratio as the IC plant. Such a plant is thought to work on the air-standard cycle. BY using this efficiency as a criterion against which to judge the measured total efficiency of the IC plant, the efficiency ratio is then taken as a measure of the fineness of performance of the plant. This is a subterfuge that by-passes the evaluation of the less readily determinable rational efficiency. Though it should be admitted that it is a clearly random process.