Ellipse Construction via Four Center Method:

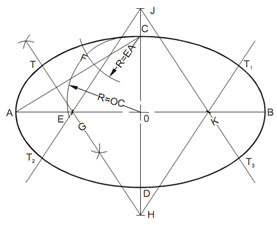
Given the major axis AB and the minor axis CD. Draw AB and CD and join A and C. With the center of the ellipse O as a center and OC as radius strike an arc intersecting OA at point E. by using C as a center and EA like radius, strike an arc intersecting the line AC at F. Sketch the perpendicular bisector of the line AF. The point G and H at that the perpendicular bisector intersect the axis AB and CD or extended are the centers of two of the arcs forming the ellipse. Situate the other two centers J and K with laying off OJ equal to OH and OK equal to OG. Along with G as center and radius GA, draw arc TAT₂, along with K as center and radius KB sketch arc T₁B T₃, with J as center and radius JD, T₂DT₃, with H as center and radius HC draw arc TCT₁. The figure, thus, formed via the four circle arcs roughly a true ellipse.