Series RLC circuits:

When the coil, capacitor, and resistor are connected in series, the resistance R can be thought of as all belonging to coil, when you use above formulas. (Thinking of it all as belonging to capacitor will work.) Then you have 2 vectors to add, while finding the impedance of a series RLC circuit:

Z = (R + jX_L) +(0 +jX_C)

= R + j(X_L+ X_C)

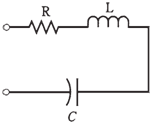
Figure--   A series RLC circuit.

Problem

A resistor, coil, and capacitor can be connected in series with R =50 Ω, X_L=22 Ω, and X_C -33 Ω. What is net impedance, Z?

Consider resistor to be part of the coil, obtaining 2 complex vectors, 50+j22 and 0-j33. Adding all these gives the resistance component of 50 + 0 = 50, and the reactive component of j22-j33 =-j11. Thus, Z= 50 - j11.