Loop Analysis of resistive circuit in the context of dc voltages and currents

The Series-parallel reduction method for analyzing DC circuits simplifies every step logically from the previous step and leads on logically to the subsequently step. Unfortunately, when the circuit is complex, this technique becomes mathematically lengthy, time consuming and probable to make mistake in computations. However, to elevate such difficulties, some techniques are available which do not need much thought at all and we require only following a well-defined faithful process. One of the most popular method is termed as ‘mesh or loop’ analysis method which based on the basic principles of circuits laws, viz., Ohm’s law and Kirchhoff’s voltage law.

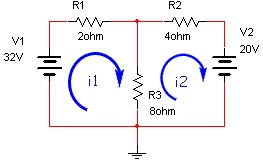
Resolving a set of equations which symbolizes a circuit is straightforward, is not always simple.  Though, developing that set of equations is not too easy.  The two generally taught techniques for forming a set of equations are the node voltage (or nodal) technique and the loop-current (or mesh) technique.  It will briefly explain each of these, and state their advantages and disadvantages. Modified Nodal Analysis which has some unique advantages.  Among its advantages is the fact that it lends itself to algorithmic solution -- the final goal of is to explain how to use a program for generating a set of equations symbolizing the circuit which can be resolved symbolically.

Circuits explained herein are simple resistive circuits with independent voltage and current sources.  The dependent sources can be added up in a straightforward way, though are not considered here.