Complex admittances in parallel:
When you see coils, resistors, and capacitors in parallel, you should envision the GB plane.
Each component, whether it is a resistor, a capacitor, or an inductor, has an admittance which can be represented as a vector in GB plane. The vectors for the pure conductances are constant, even if frequency changes. But the vectors for the coils and capacitors vary with frequency, similarly as vary in RX plane.
Pure susceptances
Pure inductive susceptances (BL) and capacitive susceptances (BC) are added together when the coils and capacitors are in parallel. Thus, B=BL = BC. Remember that BL is negative and BC is positive, just opposite from the reactances.
In GB plane, jBL and jBC vectors add, but as these vectors point in opposite directions inductive susceptance down and capacitive susceptance up the sum, jB, will point straight down or up.
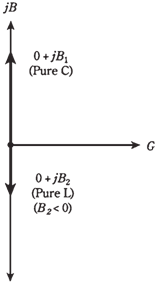
Figure Pure capacitance and pure inductance are represented by susceptance vectors which point straight up and down.
Problem 1:
A coil and capacitor are connected in parallel, with jBL j0.05 and jBC j0.08. What is the net admittance vector?
Just add the values jB = jBL + jBC = - j0.05 +j0.08 = j0.03. This is a capacitive susceptance, because it is positive imaginary. The admittance vector is 0 + j0.03.