Parallel GLC circuits:

When the coil, capacitor, and resistor are connected in parallel, resistor should be thought of a conductor, the value in siemens is equal to the reciprocal of value in ohms. Think of conductance as all belonging to the inductor. (Thinking of it all as belonging to capacitor will work.) Then you have 2 vectors to add, when finding admittance of a parallel GLC (conductance inductance capacitance) circuit:

Y = (G + jB_L) +(0 + jB_C)

  G =j(B_L + B_C)

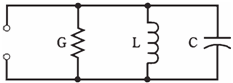
     Figure-- A parallel GLC circuit.

Problem:

A resistor, coil, and capacitor are connected in parallel with G = 0.1 siemens, jB_L= -j0.010 and jB_C = j0.020. What is net admittance vector?

Consider resistor as part of the coil, obtaining 2 complex vectors, 0.1 - j0.010 and 0 + j0.020. Adding these gives conductance component of 0.1+0.1 and the susceptance component of -j0.010 + j0.020 = j0.010. Therefore, the admittance vector is 0.1+ j0.010.