Shear Stress and Shear Strain:

Dilatation is described as change in volume (bulk) of the solid without modify of shape. If normal stress components of equal magnitude and similar nature (all tensile or all compressive) are applied on all the three mutually perpendicular planes of a solid element as shown in Figure, the solid will undergo only volume change without any change in shape. Such a state of stress (as may be obtained in the case of solid subjected to hydrostatic pressure) is called volumetric stress and the change of volume generates per unit volume of the solid is known as the volumetric strain. The ratio among volumetric stress and volumetric strain is described as Bulk Modulus.

Thus,  Bulk Modulus, K = Volumetric strain/ Volumetric Stress

in that Volumetric Strain (Change of Volume/Original Volume)

The state of stress, along with equivalent values of stress elements in all the direction is also known as spherical state of stress.

The state of deformation involving change of shape without any change of volume is defined as Distortion. Though distortion may be introduced in several ways let us consider a simple case. While shear stresses are applied on a solid as display in Figure, we search that angular deformations are introduced. The angular strain or change in angle produced is known as shear strain denoted through γ (Greek gamma) and its magnitude is expressed in radians. A ratio of the applied shear stress and the shear strain produced through it is defined as Rigidity Modulus or Shear Modulus of the material, i.e.

Rigidity Modulus, G = Shear Stress (τ) /Shear Strain (γ)

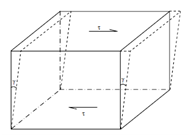
Figure: Shear Stress and Shear Strain

We have so far described four elastic constants, namely, Bulk Modulus (K), Young's Modulus (E), Poisson's Ratio (υ), and Shear Modulus (G). Later on we shall known that these four are not independent constants, but are associated to each other. We could show that there are only two independent elastic constants and the other two are dependent on them.